
分析 (1)把a=2代入函数解析式,由绝对值内的代数式等于0求得x的值,由解得的x的值把定义域分段,去绝对值后求导,利用导函数求每一段内的函数的增区间,则a=2时的函数的增区间可求;
(2)把f(x)的解析式代入g(x)=$\frac{f(x)}{x}$,利用a与1和e的大小比较去绝对值,然后求出去绝对值后的函数的导函数,利用函数的单调性求出函数在区间[1,e]上的最小值.最后把求得的函数的最小值写成分段函数的形式即可..
解答 解:(1)a=2时,f(x)=|ax-x2|+lnx=$\left\{\begin{array}{l}{2x-{x}^{2}+lnx,0<x<2}\\{{x}^{2}-2x+lnx,x≥2}\end{array}\right.$,
当0<x<2时,f′(x)=$\frac{-2{x}^{2}+2x+1}{x}$,
令f′(x)>0时,解得0<x≤$\frac{1+\sqrt{3}}{2}$,
当x≥2时,f′(x)=$\frac{2{x}^{2}-2x+1}{x}$,
令f′(x)>0时,解得x≥2,
故函数的单调增区间是(0,$\frac{1+\sqrt{3}}{2}$],[2,+∞)
(2)g(x)=|x-a|+$\frac{lnx}{x}$=$\left\{\begin{array}{l}{x-a+\frac{lnx}{x},x>a}\\{a-x+\frac{lnx}{x},0<x≤a}\end{array}\right.$,
当a≥e时,则g(x)=a-x+$\frac{lnx}{x}$,g′(x)=-1-$\frac{lnx}{{x}^{2}}$+$\frac{1}{{x}^{2}}$=$\frac{-{x}^{2}+1-lnx}{{x}^{2}}$,
令h(x)=-x2+1-lnx,则h′(x)=-2x-$\frac{1}{x}$<0
∴h(x)在[1,e]上为减函数,则h(x)≤h(1)=0.
∴g(x)在[1,e]上为减函数,得g(x)min=g(e)=a-e+$\frac{1}{e}$;
当a≤1时,∵x∈[1,e],∴0≤lnx≤1,1-lnx≥0,x2+1-lnx≥0,∴g′(x)>0.
∴g(x)在[1,e]上为增函数,
∴g(x)min=g(1)=1-a.
当1<a<e时,g(x)在[1,a]上减,[a,e]上增,
g(x)min=g(a)=$\frac{lna}{a}$
综上所述:$g{(x)_{min}}=\left\{{\begin{array}{l}{a-e+\frac{1}{e},a≥e}\\{1-a,a≤1}\\{\frac{lna}{a},1<a<e}\end{array}}\right.$
点评 本题考查了利用导数研究函数的单调性,考查了利用导数求函数在闭区间上的最值,考查了分类讨论得数学思想方法,考查了去绝对值的方法,正确的分类是解决该题的关键,属难题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
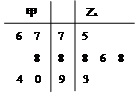 甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,
甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2x+1 | B. | y=$\frac{1}{3}$x2+1 | C. | y=-x2-x-1 | D. | y=x2-x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com