
| 1 |
| 2 |
| π |
| 4 |
| 2π |
| ω |
| 1 |
| 2 |
| π |
| 4 |
| 2π | ||
|
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| ||
| 2 |
3
| ||
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| |AB| |
| 1 |
| |MN| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解我地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下:
截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解我地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下:| 驾校A | 驾校B | 驾校C | |
| 人数 | 150 | 200 | 250 |
| 87 | 97 | 91 | 92 | 93 | 99 | 97 | 86 | 92 | 98 | 92 | 94 |
| 87 | 89 | 99 | 92 | 99 | 92 | 93 | 76 | 70 | 90 | 92 | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
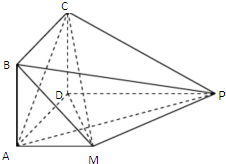 如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com