
| a |
| b |
| c |
| a |
| 2 |
| b |
| a |
| b |
| a |
| c |
| b |
| c |
| c |
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
| a |
| b |
| a |
| 2 |
| b |
| a |
| b |
| a |
| b |
| a |
| c |
| b |
| c |
| c |
| OA |
| a |
| OB |
| b |
| OC |
| c |
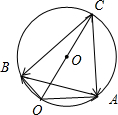
| a |
| b |
| a |
| 2 |
| b |
| a |
| b |
| a |
| b |
| ||||
|
|
| -1 | ||
|
| ||
| 2 |
| a |
| b |
| a |
| c |
| b |
| c |
| c |
| a |
| b |
|
(
|
| 5 |
|
| ||||
| sin135° |
| ||||
|
| 10 |


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
| A、2 | ||
B、2+
| ||
C、2+
| ||
| D、因为x0不唯一,故不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 |
| y |
| 10 |
 |
| i-1 |
| 10 |
 |
| i-1 |
| A、1 | B、3 | C、-3 | D、-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、若m∥n,n?α,则m∥α |
| B、若α⊥β,α∩β=m,n⊥m,则n⊥α |
| C、若l⊥n,m⊥n,则l∥m |
| D、若l⊥α,m⊥β,且l⊥m,则α⊥β |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
函数f1(x)=x3,f2(x)= ,f3(x)=
,f3(x)= ,f4(x)=
,f4(x)=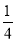 |sin(2πx)|,等差数列{an}中,a1=0,a2015=1,bn=|fk(an+1)-fk(an)|(k=1,2,3,4),用Pk表示数列{bn}的前2014项的和,则( )
|sin(2πx)|,等差数列{an}中,a1=0,a2015=1,bn=|fk(an+1)-fk(an)|(k=1,2,3,4),用Pk表示数列{bn}的前2014项的和,则( )
A.P4<1=P1=P2<P3=2 B.P4<1=P1=P2<P3<2
C.P4=1=P1=P2<P3=2 D.P4<1=P1<P2<P3=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com