
【题目】已知函数![]() 有极值,且在
有极值,且在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的极小值为
的极小值为![]() .若存在,求出实数
.若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)存在实数
(2)存在实数![]() ,使得函数
,使得函数![]() 的极小值为
的极小值为![]() .
.
【解析】试题分析:(1)![]() ,因为在
,因为在![]() 处的切线与直线
处的切线与直线![]() 垂直,所以
垂直,所以![]() ,得
,得![]() 与
与![]() 的关系
的关系![]() 。因为 函数
。因为 函数![]() 有极值,故方程
有极值,故方程![]() 有两个不等实根,其判别式大于0,结合
有两个不等实根,其判别式大于0,结合![]() ,可求实数
,可求实数![]() 的取值范围;(2)根据导函数的正负,求函数的极小值、极小值点,令极小值等于2,求得极值点,进而求实数
的取值范围;(2)根据导函数的正负,求函数的极小值、极小值点,令极小值等于2,求得极值点,进而求实数![]() 的值。
的值。
试题解析:(1)∵![]() ,∴
,∴![]() ,
,
由题意,得![]() ,∴
,∴![]() .①
.①
∵![]() 有极值,故方程
有极值,故方程![]() 有两个不等实根,
有两个不等实根,
∴![]() ,∴
,∴![]() .②
.②
由①②可得![]() ,
, ![]() 或
或![]() .
.
故实数![]() 的取僮范围是
的取僮范围是![]() .
.
(2)存在![]() .
.
∵![]() .令
.令![]() ,
, ![]() .
.
![]() ,
,![]() 随
随![]() 值的变化情况如下表:
值的变化情况如下表:
|
|
|
|
|
|
| + |
| - |
| + |
| ↑ | 极大值 | ↓ | 极小值 | ↑ |
∴![]() ,∴
,∴![]() 或
或![]() .
.
若![]() ,即
,即![]() ,则
,则![]() (舍).
(舍).
若![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴存在实数![]() ,使得函数
,使得函数![]() 的极小值为
的极小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为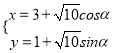 (
(![]() 为参数),以直角坐标系原点
为参数),以直角坐标系原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程,并说明其表示什么轨迹;
的极坐标方程,并说明其表示什么轨迹;
(2)若直线的极坐标方程为![]() ,求直线被曲线
,求直线被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发![]() 个红包,每个红包金额为
个红包,每个红包金额为![]() 元,
元,![]() .已知在每轮游戏中所产生的
.已知在每轮游戏中所产生的![]() 个红包金额的频率分布直方图如图所示.
个红包金额的频率分布直方图如图所示.
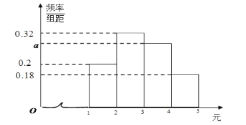
(1)求![]() 的值,并根据频率分布直方图,估计红包金额的众数;
的值,并根据频率分布直方图,估计红包金额的众数;
(2)以频率分布直方图中的频率作为概率,若甲、乙、丙三人从中各抢到一个红包,其中金额在![]() 的红包个数为
的红包个数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有极值,且在
有极值,且在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的极小值为
的极小值为![]() .若存在,求出实数
.若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 做圆
做圆![]() 的两条切线,切点为
的两条切线,切点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 是讲过定点
是讲过定点![]() 的一条直线,且与抛物线
的一条直线,且与抛物线![]() 交于
交于![]() 两点,过定点
两点,过定点![]() 作
作![]() 的垂线与抛物线交于
的垂线与抛物线交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学准备参加考试,在正式考试之前进行了十次模拟测试,测试成绩如下:
甲:137,121,131,120,129,119,132,123,125,133
乙:110,130,147,127,146,114,126,110,144,146
(1)画出甲、乙两人成绩的茎叶图,求出甲同学成绩的平均数和方差,并根据茎叶图,写出甲、乙两位同学平均成绩以及两位同学成绩的中位数的大小关系的结论;
(2)规定成绩超过127为“良好”,现在老师分别从甲、乙两人成绩中各随机选出一个,求选出成绩“良好”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于各项均为整数的数列![]() ,如果满足
,如果满足![]() (
(![]() )为完全平方数,则称数列
)为完全平方数,则称数列![]() 具有“
具有“![]() 性质”;不论数列
性质”;不论数列![]() 是否具有“
是否具有“![]() 性质”,如果存在与
性质”,如果存在与![]() 不是同一数列的
不是同一数列的![]() ,且
,且![]() 同时满足下面两个条件:①
同时满足下面两个条件:①![]() 是
是![]() 的一个排列;②数列
的一个排列;②数列![]() 具有“
具有“![]() 性质”,则称数列
性质”,则称数列![]() 具有“变换
具有“变换![]() 性质”.
性质”.
(Ⅰ)设数列![]() 的前
的前![]() 项和
项和![]() ,证明数列
,证明数列![]() 具有“
具有“![]() 性质”;
性质”;
(Ⅱ)试判断数列![]() 和数列
和数列![]() 是否具有“变换
是否具有“变换![]() 性质”,具有此性质的数列请写出相应的数列
性质”,具有此性质的数列请写出相应的数列![]() ,不具此性质的说明理由;
,不具此性质的说明理由;
(Ⅲ)对于有限项数列![]() ,某人已经验证当
,某人已经验证当![]() (
(![]() )时,数列
)时,数列![]() 具有“变换
具有“变换![]() 性质”,试证明:当
性质”,试证明:当![]() 时,数列
时,数列![]() 也具有“变换
也具有“变换![]() 性质”.
性质”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com