Question

2．在长方体ABCD-A₁B₁C₁D₁中，底面ABCD是边长为$\sqrt{2}$的正方形，AA₁=3，E是AA₁的中点，过C₁作C₁F⊥平面BDE与平面ABB₁A₁交于点F，则CF与平面ABCD所成角的正切值为$\frac{5}{6}$．

Answer 1

分析 连结AC、BD，交于点O，当C₁F与EO垂直时，C₁F⊥平面BDE，从而F∈AA₁，进而∠CAF是CF与平面ABCD所成角，由△C₁A₁F∽△EAO，求出AC，由此能求出CF与平面ABCD所成角的正切值．

解答 解：连结AC、BD，交于点O，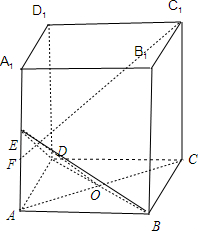
∵四边形ABCD是正方形，AA₁⊥底面ABCD，
∴BD⊥平面ACC₁A₁，
则当C₁F与EO垂直时，C₁F⊥平面BDE，
∵F∈平面ABB₁A₁，∴F∈AA₁，
∴∠CAF是CF与平面ABCD所成角，
在矩形ACC₁A₁中，△C₁A₁F∽△EAO，
则$\frac{{A}_{1}{C}_{1}}{{A}_{1}F}$=$\frac{AE}{AO}$，
∵A₁C₁=2AO=$\sqrt{2}$AB=2，AE=$\frac{3}{2}$，
∴A₁F=$\frac{4}{3}$，∴AF=$\frac{5}{3}$，
∴tan$∠CAF=\frac{AF}{AC}$=$\frac{\frac{5}{3}}{2}$=$\frac{5}{6}$．
∴CF与平面ABCD所成角的正切值为$\frac{5}{6}$．
故答案为：$\frac{5}{6}$．

点评 本题考查线面角的正切值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．