
【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为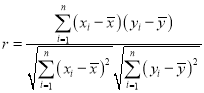 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中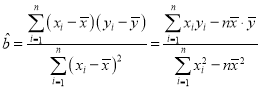 ,
,![]() .
.
参考数据:![]() ,
,![]()
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】一袋中有大小、形状相同的2个白球和10个黑球,从中任取一球.如果取出白球,则把它放回袋中;如果取出黑球,则该球不再放回,另补一个白球放到袋中.在重复![]() 次这样的操作后,记袋中的白球个数为
次这样的操作后,记袋中的白球个数为![]() .
.
(1)求![]() ;
;
(2)设![]() ,求
,求![]() ;
;
(3)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB、PA、PBC分别为⊙O的切线和割线,切点A是BD的中点,AC、BD相交于点E,AB、PE相交于点F,直线CF交⊙O于另一点G、交PA于点K.

证明:(1)K是PA的中点;(2)![]() ..
..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种设备随着使用年限的增加,每年的维护费相应增加现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如下表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
(1)在这5年中随机抽取两年,求平均每台设备每年的维护费用至少有1年多于2万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程.若该设备的价格是每台16万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?请说明理由.
的线性回归方程.若该设备的价格是每台16万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?请说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 中点现将四边形
中点现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体在图②中,
,得到如图②所示的多面体在图②中,
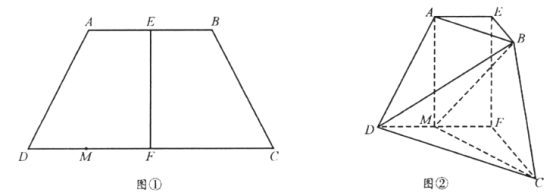
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD//BC,BC=2AD,AD⊥CD,PD⊥平面ABCD,E为PB的中点.
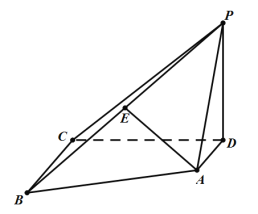
(1)求证:AE//平面PDC;
(2)若BC=CD=PD,求直线AC与平面PBC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为丰富教职工生活,五一节举办教职工趣味投篮比赛,有![]() 两个定点投篮位置,在
两个定点投篮位置,在![]() 点投中一球得2分,在
点投中一球得2分,在![]() 点投中一球得3分.规则是:每人投篮三次按先
点投中一球得3分.规则是:每人投篮三次按先![]() 再
再![]() 再
再![]() 的顺序各投篮一次,教师甲在
的顺序各投篮一次,教师甲在![]() 和
和![]() 点投中的概率分别是
点投中的概率分别是![]() 和
和![]() ,且在
,且在![]() 两点投中与否相互独立.
两点投中与否相互独立.
(1)若教师甲投篮三次,求教师甲投篮得分![]() 的分布列;
的分布列;
(2)若教师乙与教师甲在![]() 点投中的概率相同,两人按规则各投三次,求甲胜乙的概率.
点投中的概率相同,两人按规则各投三次,求甲胜乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com