
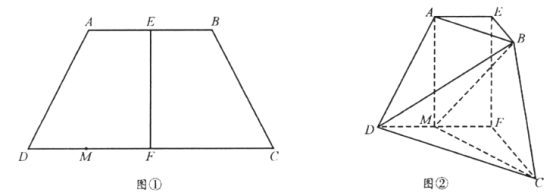
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 中点现将四边形
中点现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体在图②中,
,得到如图②所示的多面体在图②中,
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
【答案】(1)见证明;(2)![]()
【解析】
(1)由已知可得EF⊥AB,EF⊥CD,折叠后,EF⊥DF,EF⊥CF,利用线面垂直的判定得EF⊥平面DCF,从而得到EF⊥MC;(2)由平面![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() ,得
,得![]() ,进一步得
,进一步得![]() ,
,![]() ,
,![]() 两两垂直.以
两两垂直.以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,求平面
,求平面![]() ,平面
,平面![]() 的法向量,求解即可
的法向量,求解即可
(1)由题意,可知在等腰梯形![]() 中,
中,![]() ,
,
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .
.
∴折叠后,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
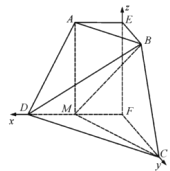
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
设平面![]() ,平面
,平面![]() 的法向量分别为
的法向量分别为
![]() ,
,![]() .
.
由 ,得
,得![]() .
.
取![]() ,则
,则![]() .
.
由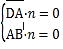 ,得
,得![]() .
.
取![]() ,则
,则![]() .
.
∵ ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,
上,![]() ,试确定
,试确定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(3)若![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有![]() 个均匀的红球和
个均匀的红球和![]() 个均匀的白球,每个球被取到的概率相等,已知从盒子里一次随机取出1个球,取到的球是红球的概率为
个均匀的白球,每个球被取到的概率相等,已知从盒子里一次随机取出1个球,取到的球是红球的概率为![]() ,从盒子里一次随机取出2个球,取到的球至少有1个是白球的概率为
,从盒子里一次随机取出2个球,取到的球至少有1个是白球的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若一次从盒子里随机取出3个球,求取到的白球个数不小于红球个数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}的前n项和为Sn,满足:对任意的n∈N*,都有an+1+Sn+1=1,又a1![]() .
.
(1)求数列{an}的通项公式;
(2)令bn=log2an,求![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为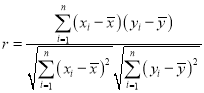 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中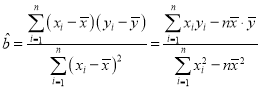 ,
,![]() .
.
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,AC⊥BC,且,AC=BC=2,D,E分别为AB,PB中点,PD⊥平面ABC,PD=3.
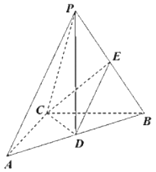
(1)求直线CE与直线PA夹角的余弦值;
(2)求直线PC与平面DEC夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:其中正确命题数是( )
A.在线性回归模型中,相关系数![]() 表示解释变量
表示解释变量![]() 对于预报变量
对于预报变量![]() 变化的贡献率,
变化的贡献率,![]() 越接近于1,表示回归效果越好
越接近于1,表示回归效果越好
B.两个变量相关性越强,则相关系数的绝对值就越接近于1
C.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位
平均减少0.5个单位
D.对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值来说,观测值越小,“
的观测值来说,观测值越小,“![]() 与
与![]() 有关系”的把握程度越大
有关系”的把握程度越大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com