
分析 (Ⅰ)根据f(2-x)=f(x+2)得出x=2是f(x)的对称轴,从而得出函数的零点,求出a、b的值;
(Ⅱ)设出函数f(x)的解析式,表示出g(x),求出g(x)的最大值h(a),再求h(a)的最小值.
解答 解:(Ⅰ)∵对任意x∈R,都有f(2-x)=f(x+2),
∴x=2是f(x)的对称轴,
∴1,3为函数的两个零点,
∴$\left\{\begin{array}{l}{a+b=0}\\{9a+3b=2}\end{array}\right.$,
解得a=$\frac{1}{3}$,b=-$\frac{1}{3}$;
∴f(x)=$\frac{1}{3}$x2-$\frac{4}{3}$x+1;
(Ⅱ)设函数f(x)=a(x-x1)(x-x2),
则g(x)=-a(x-x1)(x-x2)+2(x2-x1)=a(x2-x)(x-x1+$\frac{2}{a}$),
当x∈(x1,x2),a≥2时,
x2-x>0,x-x1+$\frac{2}{a}$>0,
∴g(x)≤a•$\frac{1}{2}$${{(x}_{2}{-x}_{1}+\frac{1}{a})}^{2}$=a+$\frac{1}{a}$+2,
当x=-$\frac{b+1}{2a}$时“=”成立;
∴h(a)=a+$\frac{1}{a}$+2,(a≥2)
∴h(a)是单调递增的函数,
∴h(a)的最小值是h(a)min=h(2)=$\frac{9}{2}$.
点评 本题考查了二次函数的图象与性质的应用问题,也考查了求函数的最值问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
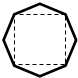 某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,则该八边形的面积的最大值为$2\sqrt{2}+2$.
某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,则该八边形的面积的最大值为$2\sqrt{2}+2$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com