
分析 由条件可知四面体的棱为长方体的面对角线,根据长方体的性质判断各结论是否正确.
解答 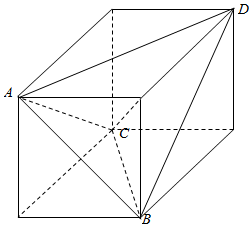 解:由条件可知四面体ABCD的四个面全等,故而①正确;
解:由条件可知四面体ABCD的四个面全等,故而①正确;
由条件可知四面体ABCD为长方体的面对角线组成的三棱锥,如图所示:
当长方体为正方体时,三棱锥任意一个顶点处的三个角均为60°,
故而从四面体ABCD每个顶点出发的三条棱两两夹角之和都是180°,故②错误;
由长方体的性质可知连结四面体ABCD每组对棱中点的线段为长方体对面的中心连线,故而③正确;
∵AC=BD,AB=CD,AD=BC,
∴过四面体任意一点的三条棱的长为△ABD的三边长,故而④正确.
故答案为:①③④.
点评 本题考查了棱锥的结构特征,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 5 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{24}$ | B. | $\frac{11}{24}$ | C. | $\frac{5}{24}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com