
| A. | $\frac{1}{24}$ | B. | $\frac{11}{24}$ | C. | $\frac{5}{24}$ | D. | $\frac{1}{2}$ |
分析 由题意得f(2017)=f(2)=$f(-3)={2^{-3}}+\int_0^{\frac{π}{6}}{cos3tdt}$,由此能求出结果.
解答 解:由题可知:当x>0时,f(x)=f(x-5),
所以f(2017)=f(2)=f(-3),
故f(2017)=$f(-3)={2^{-3}}+\int_0^{\frac{π}{6}}{cos3tdt}=\frac{1}{8}+\frac{1}{3}sin3t|_0^{\frac{π}{6}}=\frac{11}{24}$.
故选:B.
点评 本题考查函数值的求法,考查函数的周期性、定积分等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,7) | B. | (4,6) | C. | (5,5) | D. | (6,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
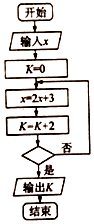
| A. | x>50? | B. | x>90? | C. | x>100? | D. | x>200? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com