
分析 欲求所围成的三角形的面积,先求出在点(1,2)处的切线方程,只须求出其斜率的值即可,故要利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
解答 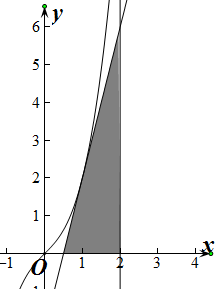 解:∵y=x3+x
解:∵y=x3+x
∴y'=3x2+1,
当x=1时,y'=4得切线的斜率为4,所以k=4;
所以曲线在点(1,2)处的切线方程为:
y-2=4×(x-1),即4x-y-2=0.
令y=0得:x=$\frac{1}{2}$,令x=2时,y=6
∴切线与x轴、直线x=2所围成的三角形的面积为:
S=$\frac{1}{2}$×(2-$\frac{1}{2}$)×6=$\frac{9}{2}$
故答案为:$\frac{9}{2}$
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
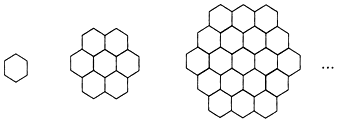 单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )
单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )| A. | 37 3n2-3n+1 | B. | 38 3n2-3n+2 | C. | 36 3n2-3n | D. | 35 3n2-3n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x)=f(x)+2 | B. | f′(x)=f(x) | C. | f′(x)=3f(x) | D. | f′(x)=2f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
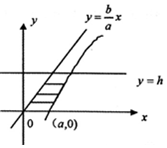 我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.
我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
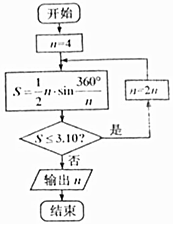 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )(参考数据:sin22.5°=0.3827,sin11.25°=0.1951,sin5.625°=0.0980)
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )(参考数据:sin22.5°=0.3827,sin11.25°=0.1951,sin5.625°=0.0980)| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com