
【题目】设a>0, ![]() 是R上的偶函数.
是R上的偶函数.
(1)求a的值;
(2)证明:f(x)在(0,+∞)上是增函数.
【答案】
(1)解:∵a>0, ![]() 是R上的偶函数.
是R上的偶函数.
∴f(﹣x)=f(x),即 ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() +a2x=
+a2x= ![]() +
+ ![]() ,
,
2x(a﹣ ![]() )﹣
)﹣ ![]() (a﹣
(a﹣ ![]() )=0,
)=0,
∴(a﹣ ![]() )(2x+
)(2x+ ![]() )=0,∵2x+
)=0,∵2x+ ![]() >0,a>0,
>0,a>0,
∴a﹣ ![]() =0,解得a=1,或a=﹣1(舍去),
=0,解得a=1,或a=﹣1(舍去),
∴a=1;
(2)证明:由(1)可知 ![]() ,
,
∴ ![]()
∵x>0,
∴22x>1,
∴f'(x)>0,
∴f(x)在(0,+∞)上单调递增
【解析】(1)根据偶函数的性质f(﹣x)=f(x),代入即可求出a的值;(2)由(1)求出了f(x)的解析式,对f(x)进行求导,证明其导数大于0即可;
【考点精析】本题主要考查了函数单调性的判断方法和函数奇偶性的性质的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】解答题
(1)设p:实数x满足(x﹣3a)(x﹣a)<0,其中a>0,q:实数x满足 ![]() ,若p是q的充分不必要条件,求实数a的取值范围;
,若p是q的充分不必要条件,求实数a的取值范围;
(2)设命题p:“函数 ![]() 无极值”;命题q:“方程
无极值”;命题q:“方程 ![]() 表示焦点在y轴上的椭圆”,若p或q为真命题,p且q为假命题,求实数m的取值范围.
表示焦点在y轴上的椭圆”,若p或q为真命题,p且q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过
经过![]() 、
、![]() ,圆心
,圆心![]() 在直线
在直线![]() 上,过点
上,过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 交圆相交于
交圆相交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)(i)请问![]() 是否为定值.若是,请求出该定值,若不是,请说明理由;
是否为定值.若是,请求出该定值,若不是,请说明理由;
(ii)若![]() 为坐标原点,且
为坐标原点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上的任意一点,设
上的任意一点,设![]() 为该圆的圆心,并且线段
为该圆的圆心,并且线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)已知![]() 两点的坐标分别为
两点的坐标分别为![]() ,
, ![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,且直线
上的一个动点,且直线![]() 分别交(1)中点
分别交(1)中点![]() 的轨迹于
的轨迹于![]() 两点(
两点(![]() 四点互不相同),证明:直线
四点互不相同),证明:直线![]() 恒过一定点,并求出该定点坐标.
恒过一定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系![]() 中,曲线
中,曲线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,直线
,直线![]() 与
与![]() 相切于
相切于![]() ,
, ![]() 为
为![]() 上任意一点,
上任意一点, ![]() 为
为![]() 在
在![]() 上的射影,
上的射影, ![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)轨迹![]() 与
与![]() 轴交于
轴交于![]() ,点
,点![]() 为曲线
为曲线![]() 上的点,且
上的点,且![]() ,
, ![]() ,试探究三角形
,试探究三角形![]() 的面积是否为定值,若为定值,求出该值;若非定值,求其取值范围.
的面积是否为定值,若为定值,求出该值;若非定值,求其取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车入住泉州一周年以来,因其“绿色出行,低碳环保”的理念而备受人们的喜爱,值此周年之际,某机构为了了解共享单车使用者的年龄段,使用频率、满意度等三个方面的信息,在全市范围内发放![]() 份调查问卷,回收到有效问卷
份调查问卷,回收到有效问卷![]() 份,现从中随机抽取
份,现从中随机抽取![]() 份,分别对使用者的年龄段、
份,分别对使用者的年龄段、![]() ~
~![]() 岁使用者的使用频率、
岁使用者的使用频率、![]() ~
~![]() 岁使用者的满意度进行汇总,得到如下三个表格:
岁使用者的满意度进行汇总,得到如下三个表格:
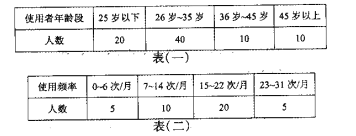
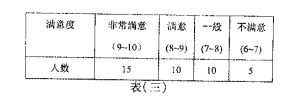
(Ⅰ)依据上述表格完成下列三个统计图形:
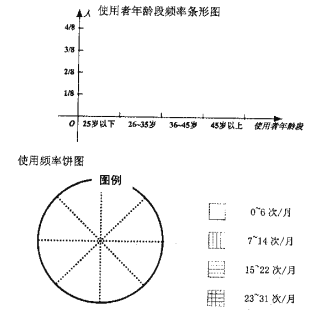
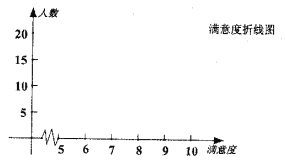
(Ⅱ)某城区现有常住人口![]() 万,请用样本估计总体的思想,试估计年龄在
万,请用样本估计总体的思想,试估计年龄在![]() 岁~
岁~![]() 岁之间,每月使用共享单车在
岁之间,每月使用共享单车在![]() ~
~![]() 次的人数.
次的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com