
分析 利用诱导公式化简可得tanα的值,根据同角三角函数关系式可得sinα,cosα的值.
解答 解:由tan(α+4π)=tan α=$\frac{sinα}{cosα}$=-$\frac{4}{3}$,
得sin α=-$\frac{4}{3}$cos α.①
又sin2 α+cos2α=1,②
由①②得$\frac{16}{9}$cos2α+cos2α=1,即cos2α=$\frac{9}{25}$.
又$α∈(\frac{π}{2},π)$,
即α是第二象限角,
∴cos α=-$\frac{3}{5}$,sin α=$\frac{4}{5}$.
点评 本题考查了诱导公式的化简能力及同角三角函数基本关系式,考查了计算能力,属于基础题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②①③ | C. | ②③① | D. | ③②① |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
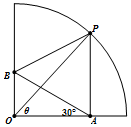 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,∠OAB=30°,∠POA=θ,记此四边形OAPB的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,∠OAB=30°,∠POA=θ,记此四边形OAPB的面积为f(θ),求f(θ)的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0或x>4} | B. | {x|x<-1或x>4} | C. | R | D. | {x|-1≤x≤0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com