
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据条件在③中令c=0得到a*b=ab+a+b从而得到f(x)的表达式,结合函数的奇偶性,单调性和最值的性质分别进行判断即可.
解答 解:①由新运算“*”的定义③令c=0,
则(a*b)*0=0*(ab)+(a*0)+(0*b)=ab+a+b,
即a*b=ab+a+b
∴f(x)=x*$\frac{1}{x}$=1+x+$\frac{1}{x}$,当x>0时,f(x)=x*$\frac{1}{x}$=1+x+$\frac{1}{x}$≥1+2$\sqrt{x•\frac{1}{x}}$=1+2=3,
当且仅当x=$\frac{1}{x}$,即x=1时取等号,∴在(0,+∞)上函数f(x)的最小值为3;故①正确,
②函数的定义域为(-∞,0)∪(0,+∞),
∵f(1)=1+1+1=3,f(-1)=1-1-1=-1,
∴f(-1)≠-f(1)且f(-1)≠f(1),则函数f(x)为非奇非偶函数,故②错误,
③函数的f′(x)=1-$\frac{1}{{x}^{2}}$,令f′(x)=0
则x=±1,
∵当x∈(-∞,-1)或(1,+∞)时,f′(x)>0
∴函数f(x)的单调递增区间为(-∞,-1)、(1,+∞).故③正确;
故正确的是①③,
故选:C
点评 本题是一个新定义运算型问题,考查了函数的最值、奇偶性、单调性等有关性质,根据条件令c=0求出函数的解析式是解决本题的关键.综合性较强,有一定的难度.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 9 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
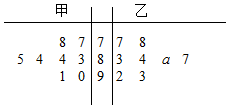 将甲、乙两名同学8次数学测验成绩统计如茎叶图所示,若乙同学8次数学测试成绩的中位数比甲同学8次数学测验成绩的平均数多1,则a=( )
将甲、乙两名同学8次数学测验成绩统计如茎叶图所示,若乙同学8次数学测试成绩的中位数比甲同学8次数学测验成绩的平均数多1,则a=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
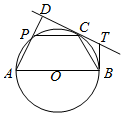 如图,AB为⊙O的直径,C为⊙O上一点(异于A、B),AD与过点C的切线互相垂直,垂足为D,AD交⊙O于点P,过点B的切线交直线DC于点T.
如图,AB为⊙O的直径,C为⊙O上一点(异于A、B),AD与过点C的切线互相垂直,垂足为D,AD交⊙O于点P,过点B的切线交直线DC于点T.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com