Question

15．设函数$f（x）=\left\{\begin{array}{l}|x|，x≤\frac{m}{2}\\{x^2}-2mx+4m，x＞\frac{m}{2}\end{array}\right.（{m∈R}）$，若存在实数t，使得函数y=f（x）-t有4个不同的零点，则m的取值范围为（$\frac{7}{2}，\frac{16}{3}$）．

Answer 1

分析 分m≤0和m＞0分别画出函数y=f（x）的图象，把函数y=f（x）-t有4个不同的零点转化为函数y=f（x）的图象与y=t有4个不同交点列关于m的不等式组求解．

解答 解：当m≤0时，函数$f（x）=\left\{\begin{array}{l}|x|，x≤\frac{m}{2}\\{x^2}-2mx+4m，x＞\frac{m}{2}\end{array}\right.（{m∈R}）$的图象如图：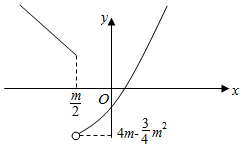

不满足题意；
当m＞0时，函数$f（x）=\left\{\begin{array}{l}|x|，x≤\frac{m}{2}\\{x^2}-2mx+4m，x＞\frac{m}{2}\end{array}\right.（{m∈R}）$的图象如图：

要使函数y=f（x）-t有4个不同的零点，
则函数y=f（x）的图象与y=t有4个不同交点，
∴$\left\{\begin{array}{l}{4m-\frac{3}{4}{m}^{2}＞0}\\{4m-{m}^{2}＜\frac{m}{2}}\end{array}\right.$，解得$\frac{7}{2}＜m＜\frac{16}{3}$．
∴m的取值范围为：（$\frac{7}{2}，\frac{16}{3}$）．
故答案为：（$\frac{7}{2}，\frac{16}{3}$）．

点评 本题考查根的存在性与根的个数判断，考查数形结合的解题思想方法，正确画出函数图象是解答该题的关键，是中档题．