
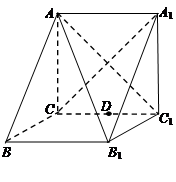
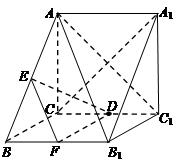
如图,在三棱柱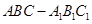 中,侧棱
中,侧棱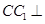 底面
底面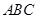 ,
,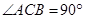 ,
,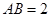 ,
,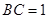 ,
,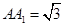 .
.
(1)证明: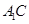
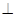 平面
平面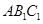 ;
;
(2)若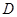 是棱
是棱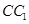 的中点,在棱
的中点,在棱 上是否存在一点
上是否存在一点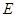 ,使
,使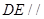 平面
平面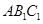 ?证明你的结论.
?证明你的结论.
(1)见解析.(2)当点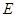 为棱
为棱 的中点时,
的中点时,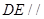 平面
平面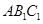 .证明见解析.
.证明见解析.
解析试题分析:(1)要证明线面垂直,须证明直线与平面内的两条相交直线都垂直,一般要遵循“先找再作”的原则,对图形进行细致分析是关键.注意到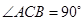 ,得到
,得到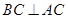 .
.
由侧棱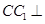 底面
底面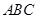 ,得到
,得到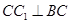 .从而得到
.从而得到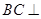 平面
平面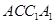 .
.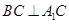 ,
,
利用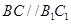 ,得到
,得到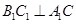 .结合四边形
.结合四边形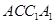 为正方形.
为正方形.
得到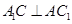 .推出
.推出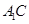
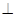 平面
平面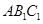 .
.
(2)对于这类存在性问题,往往是先通过对图形的分析,找“特殊点”,肯定其存在性,再加以证明.
注意到当点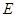 为棱
为棱 的中点时,取
的中点时,取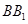 的中点
的中点 ,连
,连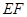 、
、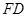 、
、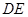 ,利用三角形相似,得到
,利用三角形相似,得到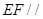 平面
平面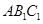 及
及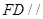 平面
平面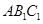 ,利用平面
,利用平面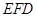
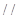 平面
平面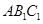 .推出
.推出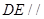 平面
平面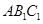 .
.
试题解析:(1)∵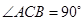 ,∴
,∴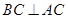 .
.
∵侧棱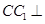 底面
底面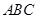 ,∴
,∴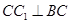 .
.
∵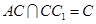 ,∴
,∴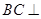 平面
平面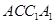 .
.
∵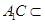 平面
平面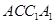 ,∴
,∴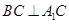 ,
,
∵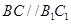 ,则
,则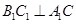 . 4分
. 4分
在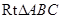 中,
中,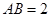 ,
,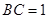 ,∴
,∴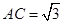 .
.
∵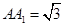 ,∴四边形
,∴四边形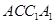 为正方形.
为正方形.
∴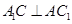 . 6分
. 6分
∵ ,∴
,∴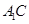
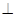 平面
平面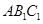 . 7分
. 7分
(2)当点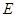 为棱
为棱 的中点时,
的中点时,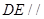 平面
平面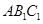 . 9分
. 9分
证明如下:
如图,取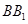 的中点
的中点 ,连
,连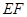 、
、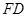 、
、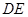 ,
,
∵

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com