

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 延长BC,作CE=AM,连接DE,则△ADM≌△DEC,再证明△MND≌△DNE,即可得到结论.
解答 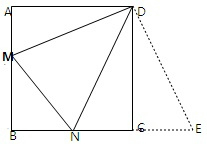 解:延长BC,作CE=AM,连接DE,则△ADM≌△DEC,
解:延长BC,作CE=AM,连接DE,则△ADM≌△DEC,
∴∠ADM=∠CDE,AD=CD,DM=DE,
∴∠MDE=∠MDC+∠CDE=∠MDC+∠ADM=$\frac{π}{2}$,
设AM=x,NC=y,则BM=2-x,BN=2-y,NE=CN+CE=x+y,
MN=△BMN周长-DB-BN=4-(2-x)-(2-y)=x+y=NE,
∴△MND≌△NDE (SSS),
∴∠MDN=∠NDE,
∴∠MDN=$\frac{1}{2}×$$\frac{π}{2}$=$\frac{π}{4}$.
故选:B.
点评 本题考查三角形的全等,考查学生数形结合思想和分析问题、解决问题的能力,属于中档题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{15}}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{2+\sqrt{15}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 6种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知△ABC中,顶点A(7,-3),AC边上的高BH所在直线方程为x-2y-5=0,AB边上的中线CM所在的直线方程为6x-y-21=0.
已知△ABC中,顶点A(7,-3),AC边上的高BH所在直线方程为x-2y-5=0,AB边上的中线CM所在的直线方程为6x-y-21=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
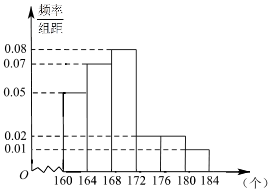 《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.
《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+y-1=0 | B. | x+3y-5=0 | C. | 3x+y-3=0 | D. | x+3y+5=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com