
| A. | [e2-1,+∞) | B. | [e2,+∞) | C. | [e2+1,+∞) | D. | [1,+∞) |
分析 函数f(x)=ex+x2-x对任意x1,x2∈[-2,2],|f(x1)-f(x2)|≤k恒成立,等价于f(x)=ex+x2-x在[-2,2]内的最大值与最小值的差小于等于k.
解答 解:∵f(x)=ex+x2-x,
∴f′(x)=ex+2x-1,
由f′(x)=ex+2x-1=0,得x=0.又f′(x)单调递增,可知f′(x)=0有唯一零点0,
∵f(-2)=$\frac{1}{{e}^{2}}$+6,f(2)=e2+2,f(0)=1.
∴函数f(x)=ex+x2-x在[-2,2]内的最大值是e2+2,最小值是1.
∴函数f(x)=ex+x2-x,对任意x1,x2∈[-2,2],|f(x1)-f(x2)|≤e2+2-1=e2+1.
∵函数f(x)=ex+x2-x对任意x1,x2∈[-2,2],|f(x1)-f(x2)|≤k恒成立,
∴k≥e2+1.
∴k的取值范围为[e2+1,+∞).
故选:C.
点评 本题考查满足条件的实数的取值范围的求法,解题的关键是要分析出|f(x1)-f(x2)|≤f(x)max-f(x)min.属于中档题


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一个圆分成6个大小不等的小扇形,取来红、黄、蓝、白、绿、黑6种颜色,如图.
一个圆分成6个大小不等的小扇形,取来红、黄、蓝、白、绿、黑6种颜色,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos2x | B. | y=sin2x | C. | y=|cosx| | D. | y=|sinx| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
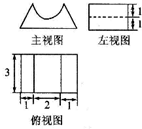
| A. | 27-$\frac{3π}{2}$ | B. | 18-$\frac{3π}{2}$ | C. | 27-3π | D. | 18-3π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com