
分析 本题以定义的一种新的变换为入手点,主要考查直线与圆的有关知识,解答本题的关键是弄懂定义的本质,由定义的新法则f:P(m,n)→P′($\sqrt{m}$,$\sqrt{n}$),(m≥0,n≥0).点A(2,6)与点B(6,2),点M是线段AB上一动点,而不难知道由变换得到点的轨迹是圆的一部分.然后根据弧长公式,易得答案
解答 解:解:由题意知AB的方程为:x+y=8,
设M(x,y),则M′(x2,y2),从而有x2+y2=8,
易知 A(2,6)→A′($\sqrt{2}$,$\sqrt{6}$),B(6,2)→B′($\sqrt{6}$,$\sqrt{2}$),
不难得出∠A′OX=$\frac{π}{3}$,∠B′OX=$\frac{π}{6}$,则∠A′OB′=$\frac{π}{6}$,点M的对应点M′所经过的路线长度为$\frac{\sqrt{2}}{3}$π.
故答案为:(2,2),$\frac{{\sqrt{2}}}{3}π$
点评 这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.弄懂定义的本质是解题关键;针对本题,通过阅读题意,不难知道由变换得到点的轨迹是圆的一部分


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 135° | C. | 45°或135° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
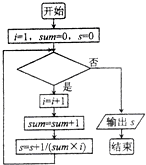
| A. | i≤5? | B. | i≤4? | C. | i≥4? | D. | i≥5? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M>N>P | B. | P<M<N | C. | N>P>M | D. | P>N>M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [e2-1,+∞) | B. | [e2,+∞) | C. | [e2+1,+∞) | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com