
分析 先求出基本事件总数n=${A}_{8}^{8}$,再求出2名中国运动员恰好抽在相邻泳道的概率为m=${A}_{2}^{2}{A}_{7}^{7}$,由此能求出2名中国运动员恰好抽在相邻泳道的概率.
解答 解:里约奥运会游泳小组赛采用抽签方法决定运动员比赛的泳道.
在由2名中国运动员和6名外国运动员组成的小组中,
基本事件总数n=${A}_{8}^{8}$,
2名中国运动员恰好抽在相邻泳道的概率为m=${A}_{2}^{2}{A}_{7}^{7}$,
∴2名中国运动员恰好抽在相邻泳道的概率为p=$\frac{m}{n}$=$\frac{{A}_{2}^{2}{A}_{7}^{7}}{{A}_{8}^{8}}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
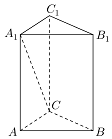 如图,已知正三棱柱ABC-A1B1C1的底面积为$\frac{{9\sqrt{3}}}{4}$,侧面积为36;
如图,已知正三棱柱ABC-A1B1C1的底面积为$\frac{{9\sqrt{3}}}{4}$,侧面积为36;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知曲线${C_1}:y=\frac{2x}{x+1}\;\;(x>0)$及曲线${C_2}:y=\frac{1}{3x}\;\;(x>0)$,C1上的点P1的横坐标为${a_1}\;(0<{a_1}<\frac{1}{2})$.从C1上的点${P_n}\;(n∈{N^*})$作直线平行于x轴,交曲线C2于Qn点,再从C2上的点${Q_n}\;(n∈{N^*})$作直线平行于y轴,交曲线C1于Pn+1点,点Pn(n=1,2,3…)的横坐标构成数列{an}.
如图,已知曲线${C_1}:y=\frac{2x}{x+1}\;\;(x>0)$及曲线${C_2}:y=\frac{1}{3x}\;\;(x>0)$,C1上的点P1的横坐标为${a_1}\;(0<{a_1}<\frac{1}{2})$.从C1上的点${P_n}\;(n∈{N^*})$作直线平行于x轴,交曲线C2于Qn点,再从C2上的点${Q_n}\;(n∈{N^*})$作直线平行于y轴,交曲线C1于Pn+1点,点Pn(n=1,2,3…)的横坐标构成数列{an}.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,4} | B. | {1,6} | C. | {2,5,7} | D. | {1,3,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com