
分析 (Ⅰ)先求导函数,再分离参数,得到$a≤\frac{1}{x}$在(0,4]上恒成立,根据函数的最值即可求出a的范围,
(Ⅱ)先求导函数,再分类讨论函数的单调性,根据函数的单调性得到函数最小值.
(Ⅲ)由(Ⅱ)可得$\frac{1}{n{e}^{n}}$=$\frac{n}{{n}^{2}{e}^{n}}$≤$\frac{1}{{n}^{2}}$•$\frac{1}{e}$,利用放缩法和裂项求和法即可证明不等式成立.
解答 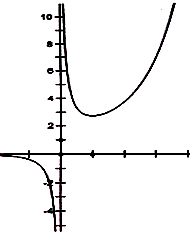 解:(Ⅰ)由题意知$f'(x)=(\frac{{{e^{ax}}}}{x})'=\frac{{{e^{ax}}(ax-1)}}{x^2}≤0$在(0,4]上恒成立.
解:(Ⅰ)由题意知$f'(x)=(\frac{{{e^{ax}}}}{x})'=\frac{{{e^{ax}}(ax-1)}}{x^2}≤0$在(0,4]上恒成立.
又eax>0,x2>0,则ax-1≤0在(0,4]上恒成立,
即$a≤\frac{1}{x}$在(0,4]上恒成立.
而当x∈(0,4]时,${(\frac{1}{x})_{min}}=\frac{1}{4}$,
所以$a≤\frac{1}{4}$,
于是实数a的取值范围是$({-∞,\frac{1}{4}}]$.
(Ⅱ)当a=1时,则$f'(x)=\frac{{{e^x}(x-1)}}{x^2}$.
当x-1>0,即x>1时,f'(x)>0;
当x-1<0且x≠0,即x<0和0<x<1时,f'(x)<0,
则f(x)的增区间为(1,+∞),减区间为(-∞,0)和(0,1).…6
据此可得函数f(x)的大致图象,如图所示:因为m>0,所以m+2>1,
①当0<m≤1时,f(x)在[m,1]上单调递减,在[1,m+2]上单调递增,所以f(x)min=f(1)=e.
②当m≥1时,f(x)在[m,m+2]上单调递增,所以$f{(x)_{min}}=f(m)=\frac{e^m}{m}$.
综上,当0<m≤1时,f(x)min=e;当m≥1时,$f{(x)_{min}}=\frac{e^m}{m}$.
证明有:(Ⅲ)由(Ⅱ)可知,当x>0时,f(x)=$\frac{{e}^{x}}{x}$≥e,
所以$\frac{x}{{e}^{x}}$≤$\frac{1}{e}$,x>0,
可得$\frac{1}{n{e}^{n}}$=$\frac{n}{{n}^{2}{e}^{n}}$≤$\frac{1}{{n}^{2}}$•$\frac{1}{e}$,
于是证:$\sum_{i=1}^{n}$$\frac{1}{i{e}^{i}}$=$\frac{1}{e}$+$\frac{1}{2{e}^{2}}$+…+$\frac{1}{n{e}^{n}}$≤$\frac{1}{e}$(1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$)<$\frac{1}{e}$(1+$\frac{1}{{2}^{2}-1}$+$\frac{1}{{3}^{2}-1}$+$\frac{1}{{n}^{2}-1}$),
=$\frac{1}{e}$[1+$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{n-2}$-$\frac{1}{n}$+$\frac{1}{n-1}$-$\frac{1}{n+1}$)],
=$\frac{1}{e}$[1+$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n}$-$\frac{1}{n+1}$)]<$\frac{1}{e}$(1+$\frac{1}{2}$+$\frac{1}{4}$)=$\frac{7}{4e}$
点评 本题考查了导数和函数的单调性和最值的关系,以及参数的取值范围,以及放缩法和裂项求和在证明数列中的应用,属于难题.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | bf(a)≤af(b) | B. | af(b)≤bf(a) | C. | bf(a)≤f(a) | D. | af(a)≤f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.
如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
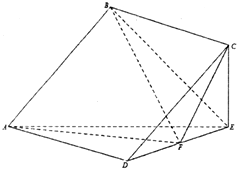 在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.
在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
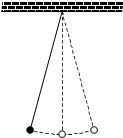 如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.
如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com