
分析 (1)求函数的导数,利用导数和单调性之间的关系进行求解即可.
(2)先求函数F(x)=f(x)-x1nx的定义域,由F(x)=0可化为a=$\frac{{e}^{x}-1}{x}$-lnx,(x>0),从而令h(x)=$\frac{{e}^{x}-1}{x}$-lnx,(x>0),求导h′(x)=$\frac{({e}^{x}-1)(x-1)}{{x}^{2}}$,从而由导数求单调性并求最值;
(3)当x>0时,ex-1>x,故对?x>0,g(x)>0;构造函数H(x)=xex-ex+1(x>0),则H′(x)=xex>0;从而由导数确定恒成立问题
解答 解:(1)∵f(x)=ex-x-1,
∴f′(x)=ex-1>0,x>0
f′(x)=ex-1<0,x<0
∴函数f(x)的单调递增区间(0.+∞);
函数f(x)的单调递减区间(-∞,0);
(2)(2)F(x)=f(x)-x1nx的定义域为(0,+∞),
由F(x)=0得,a=$\frac{{e}^{x}-1}{x}$-lnx,(x>0),
令h(x)=)=$\frac{{e}^{x}-1}{x}$-lnx,(x>0),则h′(x)=$\frac{({e}^{x}-1)(x-1)}{{x}^{2}}$,
由于x>0,ex-1>0;当x>1时,h′(x)>0;当0<x<1,h′(x)<0;
故函数h(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
故h(x)≥h(1)=e-1;
又由(1)知,当a=1时,对?x>0,有f(x)>f(lna)=0;
即ex-1>x,故$\frac{{e}^{x}-1}{x}$>1;
∵x>0,∴$\frac{{e}^{x}-1}{x}$>0,
当x→0时,lnx→-∞,∴h(x)→+∞;
当a>e-1时,函数F(x)有两个不同的零点,
当a=e-1时,函数F(x)有且级有一个零点,
当a<e-1时,函数F(x)没有零点;
(3)由(2)知,当x>0时,ex-1>x,故对?x>0,g(x)>0;
构造函数H(x)=xex-ex+1(x>0),则H′(x)=xex>0;
故函数H(x)在(0,+∞)上单调递增,
则H(x)>H(0),
则?x>0,xex-ex+1>0成立,
当a≤1时,由(1)知,f(x)在(lna,+∞)上单调递增,在(0,lna)上单调递减,
帮当0<x<lna时,0<g(x)<x<lna,
所以f(g(x))>f(x),则不满足题意,
所以满足题意的a的取值范围是(-∞,1].
点评 本题考查了导数的综合应用及恒成立问题,考查学生分析解决问题的能力,分类讨论的解题思想,属于中档题


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
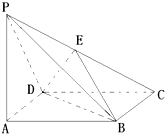 如图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,PA=a,E为CP中点,
如图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,PA=a,E为CP中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{3},\frac{{\sqrt{3}}}{2}-\frac{π}{6})$ | B. | $(-\frac{π}{3},\frac{π}{6}-\frac{{\sqrt{3}}}{2})$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com