Question

7．函数y=Asin（ωx+φ）+B的部分图象如下图所示，设A＞0，ω＞0，|φ|＜$\frac{π}{2}$，则$f（\frac{π}{3}）$=3．  

Answer 1

分析 求出函数的周期，求出ω，利用图象求出A，b，然后通过函数图象经过的特殊点求出φ即可求$f（\frac{π}{3}）$的值．

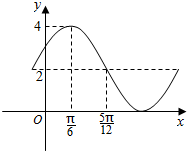
解答 解：由函数的图象可知：A=2，B=2，T=4×（$\frac{5π}{12}$-$\frac{π}{6}$）=π，所以ω=2，
因为函数的图象经过（$\frac{π}{6}$，4），
所以4=2sin（2×$\frac{π}{6}$+φ）+2，即1=sin（$\frac{π}{3}$+φ），因为|φ|＜$\frac{π}{2}$，所以φ=$\frac{π}{6}$，
所以：f（$\frac{π}{3}$）=2sin（2×$\frac{π}{3}$+$\frac{π}{6}$）+2=3，
故答案为：3．

点评 本题考查三角函数的解析式的求法，注意函数的图象的应用，考查分析问题解决问题的能力，属于中档题．