
分析 根据题意先求圆心,利用与另外一个圆相外切,求出半径,直线与圆相交建立关系.动点考查,求方程.
解答 解:由题意:圆C的圆心在直线x-y+1=0与x轴的交点,则圆心为(-1,0),设半径为r.
圆C与圆(x-2)2+(y-3)2=8相外切,圆心距等于两圆半径之和,∴r+$2\sqrt{2}$=$3\sqrt{2}$
解得:r=$\sqrt{2}$
所以圆C:(x+1)2+y2=2
P(-1,1)在圆C内.
由圆的弦长性质知道,弦长最短,对应的圆心角最小,当∠ACB最小时,弦长最短,过某点的最短弦长是与过该点的直径垂直.
∵过P(-1,1)的直径方程为x=-1,∴过P(-1,1)的最短弦方程为y=1,此时∠ACB最小.
点评 本题考查了圆与直线的关系的运用,过某点的弦长的性质.根据直线和圆相切的等价条件是解决本题的关键.属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | S12 | B. | S7 | C. | S6 | D. | S1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2+1 | B. | y=-x2+1 | C. | $y=-{x^2}+1,x∈[{-\sqrt{2},\sqrt{2}}]$ | D. | y=x2+1,x∈[-$\sqrt{2}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2016年04月13日“山东济南非法经营疫苗系列案件”披露后,引发社会高度关注,引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧.为采取后续处置措施提供依据,保障受种者的健康,尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效,对某疫苗预防疾病的效果,进行动物实验,得到统计数据如表,现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为$\frac{2}{5}$.
2016年04月13日“山东济南非法经营疫苗系列案件”披露后,引发社会高度关注,引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧.为采取后续处置措施提供依据,保障受种者的健康,尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效,对某疫苗预防疾病的效果,进行动物实验,得到统计数据如表,现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为$\frac{2}{5}$.| 未发病 | 发病 | 合计 | |
| 未注射疫苗 | 20 | x | A |
| 注射疫苗 | 30 | y | B |
| 合计 | 50 | 50 | 100 |
| P( K2≤K0) | 0.05 | 0.01 | 0.005 | 0.001 |
| K0 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
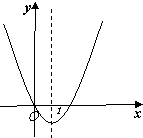 (文)二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是( )
(文)二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是( )| A. | -1≤t<3 | B. | t≥-1 | C. | 3<t<8 | D. | -1≤t<8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com