
已知椭圆 的短半轴长为
的短半轴长为 ,动点
,动点
 在直线
在直线 (
( 为半焦距)上.
为半焦距)上.
(1)求椭圆的标准方程;
(2)求以 为直径且被直线
为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;
(3)设 是椭圆的右焦点,过点
是椭圆的右焦点,过点 作
作 的垂线与以
的垂线与以 为直径的圆交于点
为直径的圆交于点 ,
,
求证:线段 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
(1) ,(2)
,(2) ,(3)
,(3)  .
.
【解析】
试题分析:(1)求椭圆标准方程,基本方法为待定系数法.由题意得 及
及 ,因此可解得
,因此可解得 ,
, .(2)圆的弦长问题,通常化为直角三角形,即半径、半弦长、圆心到直线距离构成一个直角三角形. 圆心为
.(2)圆的弦长问题,通常化为直角三角形,即半径、半弦长、圆心到直线距离构成一个直角三角形. 圆心为 ,圆心到直线
,圆心到直线 的距离
的距离 ,因此
,因此 ,
, ,所求圆的方程为
,所求圆的方程为 . (3)涉及定值问题,一般通过计算,以算代证.本题有两种算法,一是利用射影定理,只需求出点
. (3)涉及定值问题,一般通过计算,以算代证.本题有两种算法,一是利用射影定理,只需求出点 在
在 上射影
上射影 的坐标,即由两直线方程
的坐标,即由两直线方程 得
得 ,因此
,因此 .二是利用向量坐标表示,即设
.二是利用向量坐标表示,即设 ,根据两个垂直,消去参数t,确定
,根据两个垂直,消去参数t,确定 .
.
试题解析:(1)由点 在直线
在直线 上,得
上,得 ,
,
故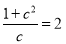 , ∴
, ∴ . 从而
. 从而 . 2分
. 2分
所以椭圆方程为 . 4分
. 4分
(2)以 为直径的圆的方程为
为直径的圆的方程为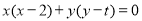 .
.
即 . 其圆心为
. 其圆心为 ,半径
,半径 . 6分
. 6分
因为以 为直径的圆被直线
为直径的圆被直线 截得的弦长为
截得的弦长为 ,
,
所以圆心到直线 的距离
的距离 .
.
所以 ,解得
,解得 .所求圆的方程为
.所求圆的方程为 . 9分
. 9分
(3)方法一:由平几知: ,
,
直线
 ,直线
,直线
 ,
,
由 得
得 .
.
∴ .
.
所以线段 的长为定值
的长为定值 . 13分
. 13分
方法二:设 ,
,
则 .
.
 .
.
又 .
.
所以, 为定值. 13分
为定值. 13分
考点:椭圆方程,圆的弦长,定值问题


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:2013-2014学年陕西省高考前30天数学保温训练10复数(解析版) 题型:选择题
已知i是虚数单位,则 =( )
=( )
A.1﹣2i B.2﹣i C.2+i D.1+2i
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省等五校高三第二次联合模拟考试文科数学试卷(解析版) 题型:选择题
已知 满足不等式
满足不等式 设
设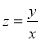 ,则
,则 的最大值与最小值的差为( )
的最大值与最小值的差为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省等五校高三第三次模拟理科数学试卷(解析版) 题型:选择题
圆 上的点到直线
上的点到直线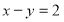 的距离最大值是( )
的距离最大值是( )
(A)2 (B)1+ (C)
(C) (D)1+
(D)1+
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省等五校高三第三次模拟文科数学试卷(解析版) 题型:填空题
在极坐标系中,若圆 的极坐标方程为
的极坐标方程为 ,若以极点为原点,以极轴为
,若以极点为原点,以极轴为 轴的正半轴建立相应的平面直角坐标系
轴的正半轴建立相应的平面直角坐标系 ,则在直角坐标系中,圆心
,则在直角坐标系中,圆心 的直角坐标是 .
的直角坐标是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省等五校高三第三次模拟文科数学试卷(解析版) 题型:选择题
定义域为 的函数
的函数 满足
满足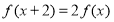 ,当
,当 时,
时, 若当
若当 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
(A) (B)
(B)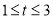 (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高考第七次适应性训练理科数学试卷(解析版) 题型:填空题
如图,已知 的直径
的直径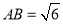 ,
, 为
为 上一点,且
上一点,且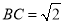 ,过点
,过点 的
的 的切线交
的切线交 延长线于点
延长线于点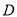 ,则
,则 ________;
________;

查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高三下学期第八次适应性训练理科数学试卷(解析版) 题型:解答题
一个袋中装有8个大小质地相同的球,其中4个红球、4个白球,现从中任意取出四个球,设X为取得红球的个数.
(1)求X的分布列;
(2)若摸出4个都是红球记5分,摸出3个红球记4分,否则记2分.求得分的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com