Question

9．如图，将长$A{A^'}=3\sqrt{3}$，宽AA₁=3的矩形沿长的三等分线处折叠成一个三棱柱，如图所示：
（1）求异面直线PQ与AC所成角的余弦值；
（2）求三棱锥A₁-APQ的体积．

Answer 1

分析 （1）在B₁B上取一点D，使得B₁D=1，连结A₁D，C₁D，即可求异面直线PQ与AC所成角的余弦值；
（2）利用等体积转化，即可求三棱锥A₁-APQ的体积．

解答 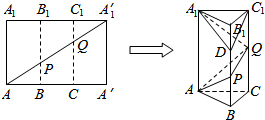解：（1）由已知，三棱柱为直三棱柱，PB=1，QC=2，
在B₁P上取一点D，使得B₁D=1，连结A₁D，C₁D，则PQ∥C₁D，
∴∠A₁C₁D为直线PQ与AC所成的角…（3分）
又A₁D=C₁D=2，A₁C₁=$\sqrt{3}$，
在△A₁C₁D中，cos∠A₁C₁D=$\frac{\sqrt{3}}{4}$，
∴直线PQ与AC所成的夹角的余弦值为$\frac{\sqrt{3}}{4}$．…（7分）
（2）△A₁AP的面积为$\frac{1}{2}×3×\sqrt{3}$=$\frac{3\sqrt{3}}{2}$，点Q到平面A₁AP的距离为$\frac{3}{2}$，
则${V}_{{A}_{1}-APQ}$=${V}_{Q-{A}_{1}AP}$=$\frac{1}{3}×\frac{3\sqrt{3}}{2}×\frac{3}{2}$=$\frac{3\sqrt{3}}{4}$．…（12分）

点评 本题考查直线PQ与AC所成的夹角的余弦值的求法，考查棱锥的体积的求法，考查学生分析解决问题的能力，正确转化是关键．