
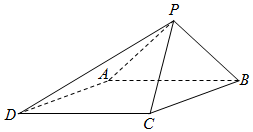
 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.分析 (Ⅰ)当m是AB的中点时,推导出AB⊥PM,AB⊥CM,从而得到AB⊥平面PCM.
(Ⅱ)取AB中点O,以O为坐标原点,以OC,OB,OP分别为x轴,y轴,z轴建立空间直坐标系O-xyz,利用向量法能求出二面角B-PC-D的余弦值.
解答 解:(Ⅰ)当m是AB的中点时,AB⊥平面PCM.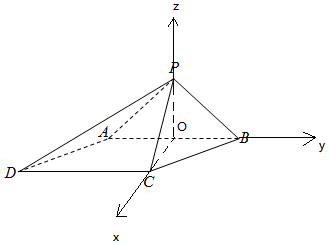
证明如下:
∵AP=PB,∴AB⊥PM…(2分)
又△ACB中,AB=BC,∠ABC=60°,
∴△ABC是正三角形,∴AB⊥CM,
又 PM∩CM=M,∴AB⊥平面PCM.…(4分)
解:(Ⅱ)取AB中点O,
由AB=PC=2,$AP=BP=\sqrt{2}$,解得PO=1,$OC=\sqrt{3}$,
∴OP2+OC2=PC2,∴OP⊥OC…(6分)
以O为坐标原点,以OC,OB,OP分别为x轴,y轴,z轴建立空间直坐标系O-xyz,
则B(0,1,0),$C(\sqrt{3},0,0)$,P(0,0,1),$D(\sqrt{3},-2,0)$,
∴$\overrightarrow{BC}=(\sqrt{3},-1,0)$,$\overrightarrow{PC}=(\sqrt{3},0,-1)$,$\overrightarrow{DC}=(0,2,0)$
设平面DCP的一个法向量为$\overrightarrow{n_1}=(1,y,z)$,则$\overrightarrow{n_1}⊥\overrightarrow{PC}$,$\overrightarrow{n_1}⊥\overrightarrow{DC}$,
∴$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{PC}=\sqrt{3}-z=0\\ \overrightarrow{n_1}•\overrightarrow{DC}=2y=0\end{array}\right.$,∴$z=\sqrt{3}$,y=0,∴$\overrightarrow{n_1}=(1,0,\sqrt{3})$…(8分)
设平面BCP的一个法向量为$\overrightarrow{n_2}=(1,b,c)$,则$\overrightarrow{n_2}⊥\overrightarrow{PC}$,$\overrightarrow{n_2}⊥\overrightarrow{BC}$,
∴$\left\{\begin{array}{l}\overrightarrow{n_2}•\overrightarrow{PC}=\sqrt{3}-c=0\\ \overrightarrow{n_2}•\overrightarrow{BC}=\sqrt{3}-b=0\end{array}\right.$,∴$c=\sqrt{3}$,$b=\sqrt{3}$,
∴$\overrightarrow{n_2}=(1,\sqrt{3},\sqrt{3})$…(10分)
∴$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}=\frac{4}{{2×\sqrt{7}}}=\frac{{2\sqrt{7}}}{7}$,
∵二面角B-PC-D为钝角,
∴二面角B-PC-D的余弦值为$-\frac{{2\sqrt{7}}}{7}$.…(12分)
点评 本题考查满足线向垂直的点的位置的确定与证明,考查二面角的余弦值的求法,是中档题,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | g(π)<g(3)<g($\sqrt{2}$) | B. | g(π)<g($\sqrt{2}$)<g(3) | C. | g($\sqrt{2}$)<g(3)<g(π) | D. | g($\sqrt{2}$)<g(π)<g(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6051 | B. | 4034 | C. | 2017 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
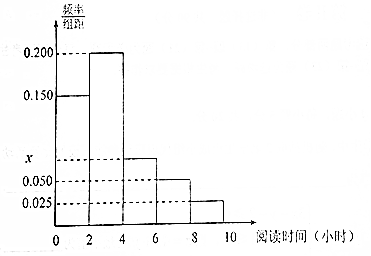 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,4} | B. | {3,4,5} | C. | {2,3,4,5} | D. | {4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com