
分析 (Ⅰ)首先,将所给曲线C的参数方程化为普通方程,然后,根据轨迹问题,确定其轨迹问题;
(Ⅱ)首先,求解圆心到直线的距离,然后,将所求的距离减去半径即可得到最短距离.
解答 解:(Ⅰ)根据曲线C的参数方程为$\left\{\begin{array}{l}{x=cosθ}\\{y=1+sinθ}\end{array}\right.$(θ为参数),得
x2+(y-1)2=1,
∵直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{3}{5}t+2}\\{y=\frac{4}{5}t}\end{array}\right.$(t为参数),
∴4x-3y-8=0,
令y=0,得到x=2,
∴A(2,0),
设点B的坐标为(x0,y0),点P的坐标为(x,y),
∴$\left\{\begin{array}{l}{x=\frac{2+{x}_{0}}{2}}\\{y=\frac{0+{y}_{0}}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{0}=2x-2}\\{{y}_{0}=2y}\end{array}\right.$,①
又∵点B(x0,y0)在圆C上,
∴x02+(y0-1)2=1,
将①代入,得
(2x-2)2+(2y)2=1,
∴(x-1)2+y2=$\frac{1}{4}$
∴线段AB的中点P的轨迹的平面直角坐标方程:(x-1)2+y2=$\frac{1}{4}$.
(Ⅱ)∵圆心(0,1)到直线的距离为$\frac{|0-3×1-8|}{\sqrt{{3}^{2}+(-4)^{2}}}$=$\frac{11}{5}$,
∴点B到直线l的最短距离$\frac{11}{5}-1$=$\frac{6}{5}$.
点评 本题重点考查了直线与圆的位置关系、点到直线的距离公式、圆的参数方程和普通方程的互化等知识,考查比较综合和灵活,掌握轨迹问题的处理思路和方法是解题的关键,属于中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
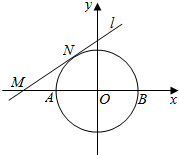 已知圆O:x2+y2=1与x轴交于A,B两点,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,且与圆O恰有两个公共点.
已知圆O:x2+y2=1与x轴交于A,B两点,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,且与圆O恰有两个公共点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
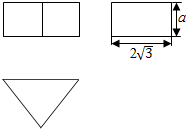
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
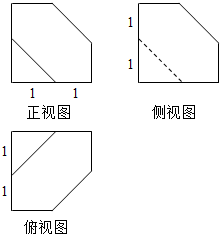
| A. | 1 | B. | 21+$\sqrt{3}$ | C. | 3$\sqrt{3}$+12 | D. | $\frac{3\sqrt{3}}{2}$+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
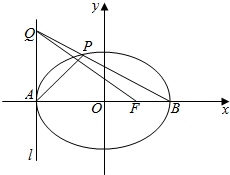 如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.
如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
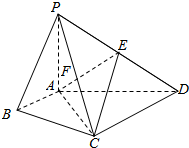 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com