
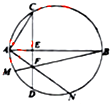
 如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.
如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.| BF |
| BA |
| BE |
| BM |
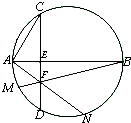 证明:(1)连结BN,则AN⊥BN,
证明:(1)连结BN,则AN⊥BN,| BF |
| BA |
| BE |
| BM |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
 某校高三年级从一次模拟考试中随机抽取50名学生(男、女生各25名),将数学成绩进行统计,所得数据的茎叶图如图所示,以组距为10将数据按[80,90),[90,100),…,[130,140),[140,150]分成七组绘制频率分布直方图,则落在区间[130,140)的小矩形的面积为( )
某校高三年级从一次模拟考试中随机抽取50名学生(男、女生各25名),将数学成绩进行统计,所得数据的茎叶图如图所示,以组距为10将数据按[80,90),[90,100),…,[130,140),[140,150]分成七组绘制频率分布直方图,则落在区间[130,140)的小矩形的面积为( )| A、1.2 | B、6 |
| C、0012 | D、0.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| f(x2)-f(x1) |
| x2-x1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com