
分析 化简可得f(x)在(-1,1)为奇函数,单调减函数且在(-1,0)时,f(x)>0,从而可得f($\frac{1}{2}$)=-1,且f($\frac{1}{{n}^{2}+n-1}$)=f($\frac{\frac{1}{n}-\frac{1}{n+1}}{1-\frac{1}{n}\frac{1}{n+1}}$)=f($\frac{1}{n}$)-f($\frac{1}{n+1}$),从而利用裂项求和法求得.
解答 解:∵函数f(x)满足$f(x)-f(y)=f(\frac{x-y}{1-xy})$,
令x=y=0得f(0)=0;
令x=0得-f(y)=f(-y).
∴f(x)在(-1,1)为奇函数,单调减函数且在(-1,0)时,f(x)>0,
则在(0,1)时f(x)<0.又f($\frac{1}{2}$)=-1,
∵f($\frac{1}{{n}^{2}+n-1}$)=f($\frac{\frac{1}{n}-\frac{1}{n+1}}{1-\frac{1}{n}\frac{1}{n+1}}$)
=f($\frac{1}{n}$)-f($\frac{1}{n+1}$),
∴m=f($\frac{1}{5}$)+f($\frac{1}{11}$)+…+f($\frac{1}{{n}^{2}+n-1}$)
=[f($\frac{1}{2}$)-f($\frac{1}{3}$)]+[f($\frac{1}{3}$)-f($\frac{1}{4}$)]+…+[f($\frac{1}{n}$)-f($\frac{1}{n+1}$)]
=f($\frac{1}{2}$)-f($\frac{1}{n+1}$)=-1-f($\frac{1}{n+1}$)>-1,
故答案为:m>-1.
点评 本题考查了学生的化简运算能力及转化思想的应用,同时考查了学生的学习能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
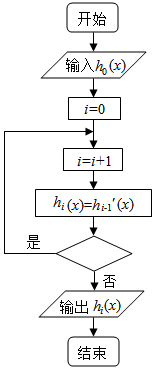 在如图所示的程序框图中(其中hi-1′(x)表示hi-1的导函数),当输入h0(x)=xex时,输出的hi(x)的结果是(x+2016)ex,则程序框图中的判断框内应填入( )
在如图所示的程序框图中(其中hi-1′(x)表示hi-1的导函数),当输入h0(x)=xex时,输出的hi(x)的结果是(x+2016)ex,则程序框图中的判断框内应填入( )| A. | i≤2014? | B. | i≤2015? | C. | i≤2016? | D. | i≤2017? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com