
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,
,![]() 为椭圆上异于长轴端点的点,且
为椭圆上异于长轴端点的点,且![]() 的最大面积为
的最大面积为![]() .
.
(1)求椭圆![]() 的标准方程
的标准方程
(2)若直线![]() 是过点
是过点![]() 点的直线,且
点的直线,且![]() 与椭圆
与椭圆![]() 交于不同的点
交于不同的点![]() 、
、![]() ,是否存在直线
,是否存在直线![]() 使得点
使得点![]() 、
、![]() 到直线
到直线![]() ,的距离
,的距离![]() 、
、![]() ,满足
,满足![]() 恒成立,若存在,求
恒成立,若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)![]() ;(2)存在,且
;(2)存在,且![]() .
.
【解析】
(1)根据题意列出有关![]() 、
、![]() 、
、![]() 的方程组,求出这三个量的值,即可得出椭圆
的方程组,求出这三个量的值,即可得出椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆方程联立,并列出韦达定理,由
的方程与椭圆方程联立,并列出韦达定理,由![]() ,得出
,得出![]() ,通过化简计算并代入韦达定理计算出
,通过化简计算并代入韦达定理计算出![]() 的值,即可得出直线
的值,即可得出直线![]() 的方程,即可说明直线
的方程,即可说明直线![]() 的存在性.
的存在性.
(1)设椭圆的焦距为![]() ,且
,且![]() 的最大面积为
的最大面积为![]() ,则
,则![]() ,
,
由已知条件得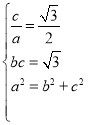 ,解得
,解得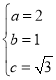 ,因此,椭圆
,因此,椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)当直线![]() 不与
不与![]() 轴重合时,设直线
轴重合时,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
将直线![]() 的方程与椭圆方程联立
的方程与椭圆方程联立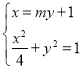 ,消去
,消去![]() 并整理得
并整理得![]() ,
,
![]() ,
,
由韦达定理得![]() ,
,![]() .
.
![]() ,即
,即![]() ,即
,即![]() ,
,
整理得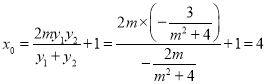 ;
;
当直线![]() 与
与![]() 轴重合时,则直线
轴重合时,则直线![]() 与椭圆
与椭圆![]() 的交点为左、右顶点,设点
的交点为左、右顶点,设点![]() 、
、![]() ,
,
![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,解得
,解得![]() .
.
综上所述,存在直线![]() ,使得
,使得![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】火箭少女101的新曲《卡路里》受到了广大听众的追捧,歌词积极向上的体现了人们对于健康以及完美身材的渴望.据有关数据显示,成年男子的体脂率在14%-25%之间.几年前小王重度肥胖,在专业健身训练后,身材不仅恢复正常,且走上美体路线.通过整理得到如下数据及散点图.
健身年数 | 1 | 2 | 3 | 4 | 5 | 6 |
体脂率 | 32 | 20 | 12 | 8 | 6.4 | 4.4 |
| 3.4 | 3 | 2.5 | 2.1 | 1.9 | 1.5 |
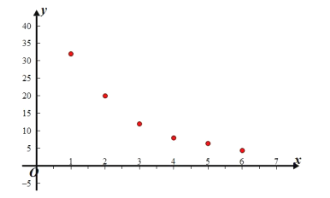
(1)根据散点图判断,![]() 与
与![]() 哪一个模型更适宜作为体脂率关于健身年数的回归方程模型(给出选择即可)
哪一个模型更适宜作为体脂率关于健身年数的回归方程模型(给出选择即可)
(2)根据(1)的判断结果与题目中所给数据,建立![]() 与
与![]() 的回归方程.(保留一位小数)
的回归方程.(保留一位小数)
(3)再坚持3年,体脂率可达到多少.
参考公式: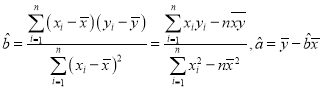
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.
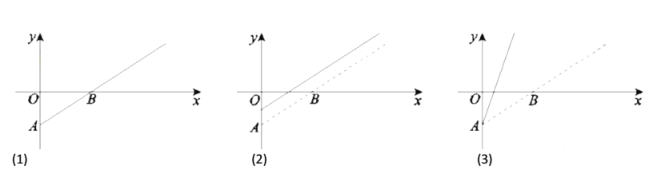
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌电脑体验店预计全年购入![]() 台电脑,已知该品牌电脑的进价为
台电脑,已知该品牌电脑的进价为![]() 元/台,为节约资金决定分批购入,若每批都购入
元/台,为节约资金决定分批购入,若每批都购入![]() (
(![]() 为正整数)台,且每批需付运费
为正整数)台,且每批需付运费![]() 元,储存购入的电脑全年所付保管费与每批购入电脑的总价值(不含运费)成正比(比例系数为
元,储存购入的电脑全年所付保管费与每批购入电脑的总价值(不含运费)成正比(比例系数为![]() ),若每批购入
),若每批购入![]() 台,则全年需付运费和保管费
台,则全年需付运费和保管费![]() 元.
元.
(1)记全年所付运费和保管费之和为![]() 元,求
元,求![]() 关于
关于![]() 的函数.
的函数.
(2)若要使全年用于支付运费和保管费的资金最少,则每批应购入电脑多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了人口规模相当的![]() 个城市采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价:
个城市采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价: ![]() (单位:元/月)和购买总人数
(单位:元/月)和购买总人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
定价x(元/月) | 20 | 30 | 50 | 60 |
年轻人(40岁以下) | 10 | 15 | 7 | 8 |
中老年人(40岁以及40岁以上) | 20 | 15 | 3 | 2 |
购买总人数y(万人) | 30 | 30 | 10 | 10 |
(Ⅰ)根据表中的数据,请用线性回归模型拟合![]() 与
与![]() 的关系,求出
的关系,求出![]() 关于
关于![]() 的回归方程;并估计
的回归方程;并估计![]() 元/月的流量包将有多少人购买?
元/月的流量包将有多少人购买?
(Ⅱ)若把![]() 元/月以下(不包括
元/月以下(不包括![]() 元)的流量包称为低价流量包,
元)的流量包称为低价流量包,![]() 元以上(包括
元以上(包括![]() 元)的流量包称为高价流量包,试运用独立性检验知识,填写下面列联,并通过计算说明是否能在犯错误的概率不超过
元)的流量包称为高价流量包,试运用独立性检验知识,填写下面列联,并通过计算说明是否能在犯错误的概率不超过![]() 的前提下,认为购买人的年龄大小与流量包价格高低有关?
的前提下,认为购买人的年龄大小与流量包价格高低有关?
定价x(元/月) | 小于50元 | 大于或等于50元 | 总计 |
年轻人(40岁以下) | |||
中老年人(40岁以及40岁以上) | |||
总计 |
参考公式:其中![]()
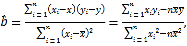
![]()
![]() 其中
其中![]()
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 是抛物线
是抛物线![]() 内一点,
内一点,![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 上任意一点,且已知
上任意一点,且已知![]() 的最小值为2.
的最小值为2.
(1)求抛物线![]() 的方程;
的方程;
(2)抛物线![]() 上一点
上一点![]() 处的切线与斜率为常数
处的切线与斜率为常数![]() 的动直线
的动直线![]() 相交于
相交于![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.问是否有常数
两点.问是否有常数![]() 使
使![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网购人数的日益增多,网上的支付方式也呈现一种多样化的状态,越来越多的便捷移动支付方式受到了人们的青睐,更被网友们评为“新四大发明”之一.随着人们消费观念的进步,许多人喜欢用信用卡购物,考虑到这一点,一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式,简单便捷,同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系,某网站对其注册用户开展抽样调查,在每个年龄段的注册用户中各随机抽取100人,得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.
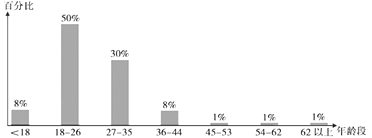
(1)由大数据可知,在18到44岁之间使用花呗“赊购”的人数百分比y与年龄x成线性相关关系,利用统计图表中的数据,以各年龄段的区间中点代表该年龄段的年龄,求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程(回归直线方程的斜率和截距保留两位有效数字);
(2)该网站年龄为20岁的注册用户共有2000人,试估算该网站20岁的注册用户中使用花呗“赊购”的人数;
(3)已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同,现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人,再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度,求抽取的两人年龄都在18到26岁的概率.
参考答案: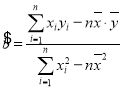 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com