
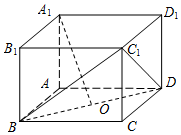
 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=$\sqrt{2}$,O为底面中心.
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=$\sqrt{2}$,O为底面中心.分析 (1)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能证明A1O⊥平面BC1D.
(2)先求出${S}_{△BD{C}_{1}}$=$\frac{1}{2}×|\overrightarrow{BD}|×|\overrightarrow{B{C}_{1}}|×sin<\overrightarrow{BD},\overrightarrow{B{C}_{1}}>$=2$\sqrt{2}$,$|\overrightarrow{{A}_{1}O}|$=2,由此能求出三棱锥A1-BC1D的体积.
解答 证明:(1)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
∵AB=AD=2,AA1=$\sqrt{2}$,O为底面中心,
∴A1(0,0,$\sqrt{2}$),O(1,1,0),B(2,0,0),D(0,2,0),C1(2,2,$\sqrt{2}$),
$\overrightarrow{{A}_{1}O}$=(1,1,-$\sqrt{2}$),$\overrightarrow{B{C}_{1}}$=(0,2,$\sqrt{2}$),$\overrightarrow{BD}$=(-2,2,0),
$\overrightarrow{{A}_{1}O}$•$\overrightarrow{B{C}_{1}}$=0+2-2=0,$\overrightarrow{{A}_{1}O}•\overrightarrow{BD}$=-2+2=0,
∴A1O⊥BC1,A1O⊥BD,
又BC1∩BD=B,∴A1O⊥平面BC1D.
解:(2)cos<$\overrightarrow{BD}$,$\overrightarrow{B{C}_{1}}$>=$\frac{\overrightarrow{BD}•\overrightarrow{B{C}_{1}}}{|\overrightarrow{BD}|•|\overrightarrow{B{C}_{1}}|}$=$\frac{4}{\sqrt{6}•\sqrt{8}}$=$\frac{1}{\sqrt{3}}$,sin<$\overrightarrow{BD},\overrightarrow{B{C}_{1}}$>=$\sqrt{1-\frac{1}{3}}$=$\frac{\sqrt{6}}{3}$,
∴${S}_{△BD{C}_{1}}$=$\frac{1}{2}×|\overrightarrow{BD}|×|\overrightarrow{B{C}_{1}}|×sin<\overrightarrow{BD},\overrightarrow{B{C}_{1}}>$=$\frac{1}{2}×\sqrt{8}×\sqrt{6}×\frac{\sqrt{6}}{3}$=2$\sqrt{2}$,
$|\overrightarrow{{A}_{1}O}|$=$\sqrt{1+1+2}=2$,
∴三棱锥A1-BC1D的体积${V}_{{A}_{1}-B{C}_{1}D}$=$\frac{1}{3}×|\overrightarrow{{A}_{1}O}|×{S}_{△BD{C}_{1}}$=$\frac{1}{3}×2×2\sqrt{2}$=$\frac{4\sqrt{2}}{3}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、空间思维能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2036 | B. | 2048 | C. | 2060 | D. | 2072 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>4+4$\sqrt{2}$ | B. | 0<m<2+2$\sqrt{2}$ | C. | 4-4$\sqrt{2}$<m<4+4$\sqrt{2}$ | D. | 0<m<4+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5和ln3可以比较大小 | |
| B. | 由平面三角形的性质,推测空间四面体的性质 | |
| C. | 东升高中高二年级有15个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人 | |
| D. | 预测股票走势图 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com