
| A. | $\frac{{π}^{2}}{4}$ | B. | $\frac{{π}^{2}}{a}$ | C. | $\frac{{π}^{2}}{2}$ | D. | π2 |
分析 利用旋转体的体积公式V=${∫}_{0}^{\frac{π}{2}}$πsin2xdx,根据定积分的运算即可求得答案.
解答 解:设所得旋转体的体积为V,
V=${∫}_{0}^{\frac{π}{2}}$πsin2xdx,
=π${∫}_{0}^{\frac{π}{2}}$$\frac{1-cos2x}{2}$dx,
=$\frac{{π}^{2}}{4}$-$\frac{π}{2}$×${∫}_{0}^{\frac{π}{2}}$cos2xdx,
=$\frac{{π}^{2}}{4}$-($\frac{π}{4}$sin2x)${丨}_{0}^{\frac{π}{2}}$,
=$\frac{{π}^{2}}{4}$,
故答案为:A.
点评 本题考查定积分的运算、定积分的应用、三角函数的导数,二倍角公式综合运用,考查数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
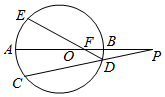 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上的一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上的一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
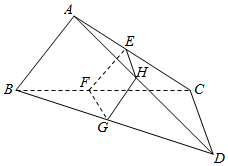 三棱锥A-BCD中,BC⊥CD,AB⊥AC,∠ABC=60°,BC=CD=2,点E,F,G分别是棱AC,BC,BD的中点,直线AD与平面EFG的交点为H.
三棱锥A-BCD中,BC⊥CD,AB⊥AC,∠ABC=60°,BC=CD=2,点E,F,G分别是棱AC,BC,BD的中点,直线AD与平面EFG的交点为H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∧(?q)是真命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨q是假命题 | D. | 命题p∨(?q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 08 | B. | 25 | C. | 41 | D. | 54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com