
分析 (1)由当n=1时,a1=S1=2a1-4,则a1=4,当n≥2时,an=Sn-Sn-1=2an-4-(2an-1-4),则an=2an-1,$\frac{{a}_{n}}{{a}_{n-1}}$=2,数列{an}是以4为首项,以2为公比的等比数列,an=4×2n=2n+1,bn+1=2n+1+2bn,$\frac{{b}_{n+1}}{{2}^{n+1}}$-$\frac{{b}_{n}}{{2}^{n}}$=1,数列{$\frac{{b}_{n}}{{2}^{n}}$}是以1为首项,以1为公差的等差数列,bn=n•2n(n∈N*);
(2)由(1)可知:bn=n•2n(n∈N*),采用“错位相减法”即可求得{bn} 的前n项和Tn.
解答 解:(1)当n=1时,a1=S1=2a1-4,则a1=4,
当n≥2时,Sn-1=2an-1-4,
an=Sn-Sn-1=2an-4-(2an-1-4),即an=2an-1,
∴$\frac{{a}_{n}}{{a}_{n-1}}$=2,
∴数列{an}是以4为首项,以2为公比的等比数列,
∴an=4×2n=2n+1,
由bn+1=an+2bn,即bn+1=2n+1+2bn,
∴$\frac{{b}_{n+1}}{{2}^{n+1}}$-$\frac{{b}_{n}}{{2}^{n}}$=1,
又$\frac{{b}_{1}}{2}$=1,
∴数列{$\frac{{b}_{n}}{{2}^{n}}$}是以1为首项,以1为公差的等差数列,
∴$\frac{{b}_{n}}{{2}^{n}}$=1+(n-1)•1=n,
∴bn=n•2n(n∈N*);
(2)由(1)可知:Tn=1×2+2×22+…+n•2n
则2Tn=1×22+…+(n-1)•2n+n•2n+1
两式相减得:-Tn=(2+22+…+2n)-n•2n+1,
=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1,
=-(n-1)•2n+1-2(n∈N*),
∴Tn=(n-1)•2n+1+2,
∴{bn} 的前n项和Tn,Tn=(n-1)•2n+1+2,(n∈N*).
点评 本题考查等差数列前n项和公式,考查等比数列与等差数列的综合应用,考查“错位相减法”求数列的前n项和的应用,考查计算能力,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 明天上午下雨,下午不下雨 | |
| B. | 明天下雨的概率为80% | |
| C. | 明天有的地方下雨,有的地方不下雨 | |
| D. | 明天下雨的时间一共是19.2小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
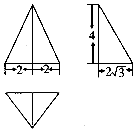
| A. | $4\sqrt{3}+8+2\sqrt{19}$ | B. | $4\sqrt{3}+8+4\sqrt{19}$ | C. | $8\sqrt{3}+8+4\sqrt{19}$ | D. | $8\sqrt{3}+8+2\sqrt{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com