
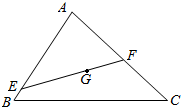
 如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.
如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值. 分析 由E,G,F三点共线,从而有向量共线,由两个向量共线定理找到向量的等式,再由三角形法则转化为用$\overrightarrow{AB}$,$\overrightarrow{AC}$表达,即可找出m,n的关系.
解答 解:∵E,G,F三点共线,
∴$\overrightarrow{AG}$=x$\overrightarrow{AE}$+(1-x)$\overrightarrow{AF}$,
即$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=xm$\overrightarrow{AB}$+(1-x)n$\overrightarrow{AC}$,
∴$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$=xm$\overrightarrow{AB}$+(1-x)n$\overrightarrow{AC}$,
∵$\overrightarrow{AB}$,$\overrightarrow{AC}$不共线,
∴$\left\{\begin{array}{l}{xm=\frac{1}{3}}\\{(1-x)n=\frac{1}{3}}\end{array}\right.$,
∴x=$\frac{1}{3m}$,1-x=$\frac{1}{3n}$,
∴$\frac{1}{3m}$+$\frac{1}{3n}$=1,
∴$\frac{1}{m}$+$\frac{1}{n}$=3.
点评 本题考查三点共线、向量共线的条件、向量的三角形法则和向量的表示等知识.抓住E、G、F三点共线,转化为向量共线是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com