
建造一条防洪堤,其断面为等腰梯形,腰与底边成角为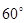 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为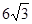 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段 与两腰长的和)要最小.
与两腰长的和)要最小.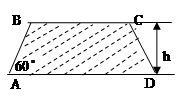
(1)求外周长的最小值,并求外周长最小时防洪堤高h为多少米?
(2)如防洪堤的高限制在 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:解答题
已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将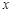 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
| 运输工具 | 运输费单价:元/(吨•千米) | 冷藏费单价:元/(吨•时) | 固定费用:元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |
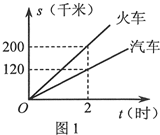
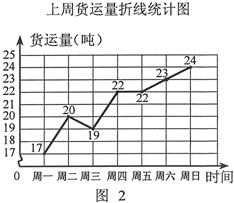
 汽(元)和
汽(元)和 火(元),分别求
火(元),分别求 汽、
汽、 火与
火与 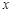 的函数关系式(不必写出
的函数关系式(不必写出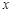 的取值范围),及
的取值范围),及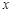 为何值时
为何值时 汽>
汽> 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交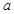 元(
元(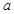 为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与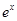 (e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com