
分析 由已知向量的坐标求得两向量的模及数量积,代入数量积求夹角公式得答案.
解答 解:∵$\overrightarrow a$=$({-1,\left.{\sqrt{3}})},\right.\overrightarrow b$=$({\sqrt{3},\left.{-1})}\right.$,
∴$\overrightarrow{a}•\overrightarrow{b}=-2\sqrt{3}$,$|\overrightarrow{a}|=|\overrightarrow{b}|=2$,
则cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{-2\sqrt{3}}{2×2}=-\frac{\sqrt{3}}{2}$,
∴$\overrightarrow a$与$\overrightarrow b$的夹角等于$\frac{5π}{6}$.
故答案为:$\frac{5π}{6}$.
点评 本题考查平面向量的数量积运算,考查了由数量积求向量的夹角,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
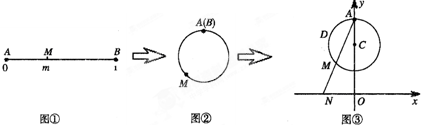
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [-2,0]和[2,+∞) | C. | [1,2]与[3,+∞) | D. | [0,2]∪(-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
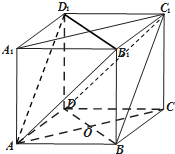 在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.
在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,+∞) | C. | (-2,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com