
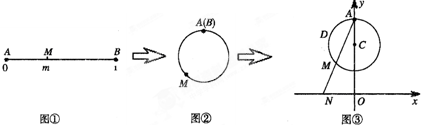
分析 借助于图形来看四个选项,先利用f($\frac{1}{4}$)=-1,判断出①错;
在有实数m所在区间(0,1)不关于原点对称,知②错;
从图形上可得f(x)在定义域上单调递增,③对;
先找到f($\frac{1}{2}$)=0,再利用图形判断④对
解答 解:如图,(1)方程f(x)=0,即N(0,0),M在A的正下方,
即有AM的弧长为$\frac{1}{2}$,即m=$\frac{1}{2}$,解得x=$\frac{1}{2}$;
(2)因为M在以(1,1-$\frac{1}{2π}$)为圆心,$\frac{1}{2π}$为半径的圆上运动,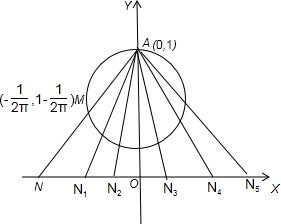
对于①当m=$\frac{1}{4}$时.M的坐标为($-\frac{1}{2π}$,1-$\frac{1}{2π}$),直线AM方程y=x+1,
所以点N的坐标为(-1,0),故f($\frac{1}{4}$)=-1,即①错.
对于②,因为实数m所在区间(0,1)不关于原点对称,
所以f(x)不存在奇偶性.故②错.
对于③,当实数m越来越大时,
如图直线AM与x轴的交点N(n,0)也越来越往右,
即n也越来越大,所以f(x)在定义域上单调递增,即③对.
对于④当实数m=$\frac{1}{2}$时,对应的点在点A的正下方,
此时点N(0,0),所以f($\frac{1}{2}$)=0,
再由图形可知f(x)的图象关于点($\frac{1}{2}$,0)对称,即④对.
故答案为:$\frac{1}{2}$; ③④.
点评 本题考查了在新定义的条件下解决函数问题,是一道很好的题.关于新定义型的题,关键是理解定义,并会用定义来解题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2015 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | h(t)=$sint,t∈[{0,\frac{π}{2}}]$ | B. | h(t)=sint,t∈[0,π] | ||
| C. | h(t)=sint,t∈[-$\frac{π}{2}$,$\frac{π}{2}$] | D. | h(t)=$\frac{1}{2}$sint,t∈[0,2π] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 7或-8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A={x|x≥0},B=R,f:求算术平方根 | B. | A=R,B=R,f:取绝对值 | ||
| C. | A=R,B=R,f:取倒数 | D. | A=R+,B=R,f:求平方 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com