
| A. | m<0 | B. | 0<m<1 | C. | m=1 | D. | m>1 |
分析 作函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≤0}\\{{x}^{2}-2x+1,}&{x>0}\end{array}\right.$的图象,从而利用数形结合的方法求解即可.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≤0}\\{{x}^{2}-2x+1,}&{x>0}\end{array}\right.$的图象如下,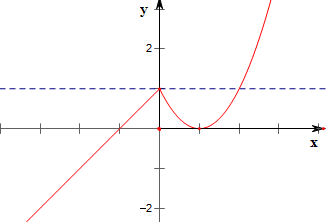
结合图象可知,当m<0时,f(x)=m有且只有一个解,
故方程f[f(x)]=m至多有三个解,故排除A;
当0<m<1时,f(x)=m有且只有三个解,
且分别在区间(-1,0),(0,1),(1,2)内,
故方程f[f(x)]=m有且只有5个解,
故选B.
点评 本题考查了方程的根与函数的零点的关系应用及数形结合的思想应用.


科目:高中数学 来源: 题型:解答题
 某建筑工地在一块唱AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为x米.
某建筑工地在一块唱AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为x米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -5 | C. | -4 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3${\;}^{\frac{2}{x}}$ | B. | y=$\sqrt{{2}^{x}-1}$ | C. | y=$\sqrt{{2}^{x}+1}$ | D. | y=($\frac{1}{2}$)2-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{lo{g}_{60}x}$ | B. | $\frac{1}{lo{g}_{3}x•lo{g}_{4}x•lo{g}_{5}x}$ | ||
| C. | $\frac{1}{lo{g}_{x}60}$ | D. | $\frac{12}{lo{g}_{3}x+lo{g}_{4}x+lo{g}_{5}x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com