
【题目】设数列![]() 是公差大于
是公差大于![]() 的等差数列,
的等差数列, ![]() 为数列
为数列![]() 的前
的前![]() 项和.已知
项和.已知![]() ,且
,且![]() 构成等比数列.
构成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,证明:
项和,证明: ![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)(1)利用等差数列前n项和、通项公式和等比数列,列出方程组,求出首项与公差,由此能求出数列{an}的通项公式.
(2)推导出bn=![]() =(2n-1)
=(2n-1) ![]() ,利用错位相减法求出数列{bn}的前n项和,由此能证明Tn<6.
,利用错位相减法求出数列{bn}的前n项和,由此能证明Tn<6.
试题解析:
(1)设数列{an}的公差为d,则d>0.
因为S3=9,所以a1+a2+a3=3a2=9,即a2=3.
因为2a1,a3-1,a4+1构成等比数列,
所以(2+d)2=2(3-d)(4+2d),
所以d=2.所以an=a2+(n-2)d=2n-1.
(2)证明:因为![]() =2n-1(n∈N*),所以bn=
=2n-1(n∈N*),所以bn=![]() =(2n-1)
=(2n-1) ![]() ,
,
所以Tn=1×![]() +3×
+3×![]() +…+(2n-1)×
+…+(2n-1)×![]() ,①
,①
所以![]() Tn=1×
Tn=1×![]() +3×
+3×![]() +…+(2n-3)×
+…+(2n-3)×![]() +(2n-1)×
+(2n-1)×![]() ,②
,②
由①②两式相减得![]() Tn=1+2×
Tn=1+2×![]() +2×
+2×![]() +…+2×
+…+2×![]() -(2n-1)×
-(2n-1)×![]() =1+
=1+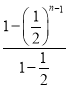 -
-![]() =3-
=3-![]() -
-![]() ,整理化简得Tn=6-
,整理化简得Tn=6-![]() .又因为n∈N*,所以Tn=6-
.又因为n∈N*,所以Tn=6-![]() <6.
<6.
点睛:用错位相减法求和应注意的问题:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.


科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神舟十一号”飞船进行新产品搭载实验,计划搭载新产品![]() ,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:
,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:
因素 | 产品 | 产品 | 备注 |
研制成本、搭载费用之和/万元 | 20 | 30 | 计划最大投资 |
金额300万元产品质量/千克 | 10 | 5 | 最大搭载 |
质量110千克预计收益/万元 | 80 | 60 | —— |
则使总预计收益达到最大时, ![]() 两种产品的搭载件数分别为( )
两种产品的搭载件数分别为( )
A. 9,4 B. 8,5 C. 9,5 D. 8,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从集合![]() 中任取三个不同的元素作为直线
中任取三个不同的元素作为直线![]() 中
中![]() 的值,若直线
的值,若直线![]() 倾斜角小于
倾斜角小于![]() ,且
,且![]() 在
在![]() 轴上的截距小于
轴上的截距小于![]() ,那么不同的直线
,那么不同的直线![]() 条数有( )
条数有( )
A. 109条B. 110条C. 111条D. 120条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究发现,北京 PM 2.5 的重要来源有土壤尘、燃煤、生物质燃烧、汽车尾气与垃圾焚烧、工业污染和二次无机气溶胶,其中燃煤的平均贡献占比约为 18%.为实现“节能减排”,还人民“碧水蓝天”,北京市推行“煤改电”工程,采用空气源热泵作为冬天供暖.进入冬季以来,该市居民用电量逐渐增加,为保证居民取暖,市供电部门对该市 100 户居民冬季(按 120 天计算)取暖用电量(单位:度)进行统计分析,得到居民冬季取暖用电量的频率分布直方图如图所示.

(1)求频率分布直方图中![]() 的值;
的值;
(2)从这 100 户居民中随机抽取 1 户进行深度调查,求这户居民冬季取暖用电量在[3300,3400]的概率;
(3)在用电量为[3200,3250),[3250,3300),[3300,3350),[3350,3400]的四组居民中,用分层抽样的方法抽取 34 户居民进行调查,则应从用电量在[3200,3250)的居民中抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表数据为某地区某种农产品的年产量![]() (单位:吨)及对应销售价格
(单位:吨)及对应销售价格![]() (单位:千元/吨).
(单位:千元/吨).
| 1 | 2 | 3 | 4 | 5 |
| 70 | 65 | 55 | 38 | 22 |
(1)若![]() 与
与![]() 有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出
有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该农产品每吨的成本为13.1千元,假设该农产品可全部卖出,利用上问所求的回归方程,预测当年产量为多少吨时,年利润![]() 最大?
最大?
(参考公式:回归直线方程为![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为直线的倾斜角,且
为直线的倾斜角,且![]() ),以原点
),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 经过圆
经过圆![]() 的圆心,求直线
的圆心,求直线![]() 的倾斜角;
的倾斜角;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,点
,点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com