
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
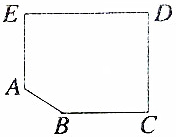 某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)
某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com