
分析 (1)将a=2代入f(x),通过讨论x的范围,求出各个区间上的x的范围,取交集即可;
(2)问题转化为:[f(x)+g(x)]min≤2$\sqrt{6}$+3,设h(x)=f(x)+g(x)=|x-1|+2|x-a|,通过讨论a的范围,求出h(x)的最小值,从而求出a的范围即可.
解答 解:(1)若a=2,f(x)-g(x)=|x-1|-2|x-2|=$\left\{\begin{array}{l}{x-3,x≤1}\\{3x-5,1<x<2}\\{-x+3,x≥2}\end{array}\right.$,
①当x≤1时,若f(x)-g(x)≤x-3,
则x-3≤x-3,故x≤1,
②当1<x<2时,若f(x)-g(x)≤x-3,
则3x-5≤x-3,即x≤1,这与1<x<2矛盾,
③当x≥2时,若f(x)-g(x)≤x-3,
则-x+3≤x-3,即x≥3,故x≥3,
综上,不等式f(x)-g(x)≤x-3的解集是{x|x≤1或x≥3};
(2)∵$\frac{{m}^{2}+m+4}{m-1}$=m-1+$\frac{6}{m-1}$+3≥2$\sqrt{6}$+3,(m>1),
当且仅当m-1=$\frac{6}{m-1}$即m=$\sqrt{6}$+1时“=”成立,
原命题等价于?x∈R,f(x)+g(x)≤2$\sqrt{6}$+3成立,
即[f(x)+g(x)]min≤2$\sqrt{6}$+3,
设h(x)=f(x)+g(x)=|x-1|+2|x-a|,
①当a<1时,h(x)=f(x)+g(x)=|x-1|+2|x-a|=$\left\{\begin{array}{l}{-3x+2a+1,x≤a}\\{x-2a+1,a<x<1}\\{3x-2a-1,x≥1}\end{array}\right.$.
h(x)min=h(a)=|a-1|=1-a,
由1-a≤2$\sqrt{6}$+3,解得:a≥-2-2$\sqrt{6}$,
∴-2-2$\sqrt{6}$≤a<1;
②当a=1时,h(x)=3|x-1|,
h(x)min=0≤2$\sqrt{6}$+3显然成立,
③当a>1时,h(x)=f(x)+g(x)=|x-1|+2|x-a|=$\left\{\begin{array}{l}{-3x+2a+1,x≤1}\\{-x+2a-1,1<x<a}\\{3x-2a-1,x≥a}\end{array}\right.$,
h(x)min=h(a)=|a-1|=a-1,
由a-1≤2$\sqrt{6}$+3,解得:a≤2$\sqrt{6}$+4,
∴1<a≤2$\sqrt{6}$+4,
综上,a的范围是[-2-2$\sqrt{6}$,4+2$\sqrt{6}$].
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及转化思想,考查运算能力,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | a=1,φ=$\frac{π}{3}$ | B. | a=1,φ=$\frac{π}{6}$ | C. | a=$\sqrt{3}$,φ=$\frac{π}{3}$ | D. | a=$\sqrt{3}$,φ=$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
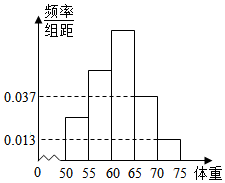 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32}{5}$ | B. | 4 | C. | $\frac{16}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com