
分析 利用同角三角函数关系式可求sinA,由余弦定理解得bc,利用三角形面积公式即可得解.
解答 解:△ABC中,∵a=1,b+c=$\sqrt{6}$,且cosA=$\frac{1}{4}$,可得:sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{15}}{4}$,
∴由余弦定理a2=b2+c2-2bccosA,可得:1=b2+c2-$\frac{1}{2}$bc=(b+c)2-$\frac{5}{2}$bc=6-$\frac{5}{2}$bc,解得:bc=2.
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×$2×$\frac{\sqrt{15}}{4}$=$\frac{\sqrt{15}}{4}$.
故答案为:$\frac{\sqrt{15}}{4}$.
点评 本题主要考查了同角三角函数关系式,余弦定理,三角形面积公式的应用,属于基本知识的考查.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
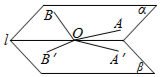 如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )
如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )| A. | ∠A′OB′为钝角 | B. | ∠A′OB′>∠AOB | ||
| C. | ∠AOB+∠AOA′<π | D. | ∠B′OB+∠BOA+∠AOA′>π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8个 | B. | 4个 | C. | 2个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com