
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
分析 由椭圆的焦点坐标,则两个交点分别为(-c,-2c),(c,2c),代入椭圆方程,根据椭圆的性质及离心率公式,即可求得椭圆的离心率.
解答 解:椭圆的焦点在x轴上,F1(-c,0),F2(c,0),则两个交点分别为(-c,-2c),(c,2c),
代入椭圆$\frac{{c}^{2}}{{a}^{2}}+\frac{4{c}^{2}}{{b}^{2}}=1$,整理得:c2(b2+4a2)=a2b2
∵b2=a2-c2,整理得:c4-6a2c2+a4=0,
由e=$\frac{c}{a}$,整理得:e4-6e2+1=0,解得:e2=3±2$\sqrt{2}$,
∵0<e<1,则e2=3-2$\sqrt{2}$=($\sqrt{2}$-1)2,
∴e=$\sqrt{2}$-1,
故选B.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查椭圆的离心率公式,考查计算能力,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
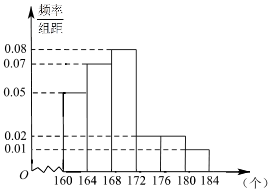 《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.
《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a>1时,函数y=ax是增函数,因为2>l,所以函数y=2x是增函数.这种推理是合情推理 | |
| B. | 在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c,则a∥c,将此结论放到空间中也是如此.这种推理是演绎推理 | |
| C. | 若分类变量X与Y的随机变量K2的观测值k越小,则两个分类变量有关系的把握性越小 | |
| D. | $\int_{-1}^1{{x^3}dx=\frac{1}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+y-1=0 | B. | x+3y-5=0 | C. | 3x+y-3=0 | D. | x+3y+5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com