
| A. | (-$\frac{π}{4}$,0) | B. | (-$\frac{π}{6}$,0) | C. | ($\frac{π}{3}$,0) | D. | ($\frac{5π}{12}$,0) |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,求得所得的图象的一个中心对称中心.
解答 解:将函数y=2cos(4x+$\frac{π}{6}$)向左平移$\frac{π}{12}$个单位后,
得到的y=2cos(4x+$\frac{π}{3}$+$\frac{π}{6}$)=-2sin4x的图象,
令4x=kπ,求得x=$\frac{kπ}{4}$,k∈Z,令k=-1,
可得可得该函数的图象的一个中心对称中心为(-$\frac{π}{4}$,0),
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ρcos θ=2$\sqrt{3}$ | B. | ρsin θ=2$\sqrt{3}$ | C. | ρcos θ=$\sqrt{3}$ | D. | ρsin θ=$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$i | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
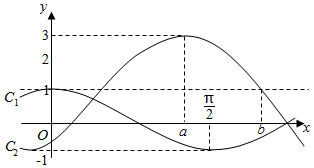 函数f(x)=Asin($ωx-\frac{π}{3}$)+1(A>0,ω>0)与g(x)=cosωx的部分图象如图所示.
函数f(x)=Asin($ωx-\frac{π}{3}$)+1(A>0,ω>0)与g(x)=cosωx的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com