
分析 根根线段AB的垂直平分线过圆的圆心,且和直线AB垂直,求出圆心坐标和直线的斜率即可得到线段AB的垂直平分线的方程,求出圆心到直线AB的距离d,利用勾股定理,求出弦长|AB|.
解答 解:∵A、B是直线3x+4y+3=0与圆x2+y2+4y=0的两个交点,
∴线段AB的垂直平分线过圆的圆心,且和直线AB垂直,
则垂直平方线的斜率k=$\frac{4}{3}$,
圆的标准方程是x2+(y+2)2=4,
则圆心坐标为(0,-2),半径R=2,
则垂直平分线的方程为y+2=$\frac{4}{3}$x,即4x-3y-6=0,
圆心到直线AB的距离d=$\frac{|0-8+3|}{\sqrt{9+16}}$=1,∴|AB|=2$\sqrt{{2}^{2}-{1}^{2}}$=2$\sqrt{3}$.
故答案为:4x-3y-6=0,2$\sqrt{3}$.
点评 本题主要考查直线和圆的位置关系的应用,利用AB垂直平分线的性质是解决本题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
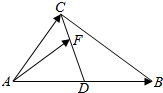 如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )| A. | 9 | B. | 10 | C. | $6+4\sqrt{2}$ | D. | $9+4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [0,2) | C. | (2,+∞) | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A组 | B组 | C组 | |
| 疫苗有效 | 903 | x | y |
| 疫苗无效 | 197 | 90 | z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com