
分析 (Ⅰ)由题意知$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}q+{a}_{1}{q}^{2}=7}\\{{a}_{1}+{a}_{1}q+5=2{a}_{1}{q}^{2}}\end{array}\right.$,从而求得;
(Ⅱ)化简bn=log2an+1=n,cn=$\frac{1}{{{b_n}{b_{n+1}}}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,从而化简不等式为k≥$\frac{n}{(n+1)(n+4)}$=$\frac{1}{n+\frac{4}{n}+5}$恒成立;从而求得.
解答 解:(Ⅰ)设等比数列{an}的公比为q,
则$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}q+{a}_{1}{q}^{2}=7}\\{{a}_{1}+{a}_{1}q+5=2{a}_{1}{q}^{2}}\end{array}\right.$,
解得,a1=1,q=2或q=-$\frac{2}{3}$(舍去);
故an=2n-1;
(Ⅱ)bn=log2an+1=n,
cn=$\frac{1}{{{b_n}{b_{n+1}}}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
故Tn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{n}{n+1}$,
要使Tn≤k(n+4)恒成立,
即k≥$\frac{n}{(n+1)(n+4)}$=$\frac{1}{n+\frac{4}{n}+5}$恒成立;
而n+$\frac{4}{n}$+5≥9,(当且仅当n=2时,等号成立);
故$\frac{1}{n+\frac{4}{n}+5}$≤$\frac{1}{9}$;
故实数k的取值范围为[$\frac{1}{9}$,+∞).
点评 本题考查了等比数列与等差数列的应用,同时考查了基本不等式与恒成立问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | (0,1) | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
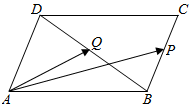 在边长为2的菱形ABCD中,∠BAD=60°,P,Q分别是BC,BD的中点,则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$.
在边长为2的菱形ABCD中,∠BAD=60°,P,Q分别是BC,BD的中点,则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-2$\sqrt{2}$ | B. | 3$+2\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$] | B. | (0,$\frac{1}{2}$) | C. | [$\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com