
分析 (1)设g(x)=ax2+bx+c,根据g(x-1)+g(1-x)=x2-2x-1直接可得答案.
(2)表示出函数f(x)的解析式,对m进行大于0、小于、和等于0进行分析可得答案.
(3)先根据H(x)的导数小于等于0判断出H(x)单调递减的,只要证明|H(m)-H(1)|<1即可.
解答 解:(1)设g(x)=ax2+bx+c,
由g(x)=g(1-x),则对称轴是x=-$\frac{b}{2a}$=$\frac{1}{2}$,
由g(x)的最小值为-$\frac{9}{8}$,
得g(x)=a${(x-\frac{1}{2})}^{2}$-$\frac{9}{8}$,由g(1)=-1,
得g(1)=$\frac{1}{4}$a-$\frac{9}{8}$=-1,解得:a=$\frac{1}{2}$,
故g(x)=$\frac{1}{2}$${(x-\frac{1}{2})}^{2}$-$\frac{9}{8}$=$\frac{1}{2}$x2-$\frac{1}{2}$x-1;
(2)f(x)=g(x+$\frac{1}{2}$)+mlnx+$\frac{9}{8}$=$\frac{1}{2}$x2+mlnx(m∈R,x>0).
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,f(x)=$\frac{1}{2}$x2>0对?x>0,f(x)>0恒成立;
当m<0时,由f′(x)=x+$\frac{m}{x}$=0⇒x=$\sqrt{-m}$,
故f(x)在(0,$\sqrt{-m}$)递减,在($\sqrt{-m}$,+∞)递增,
这时,[f(x)]min=f($\sqrt{-m}$)=-$\frac{m}{2}$+mln$\sqrt{-m}$,
[f(x)]min>0?$\left\{\begin{array}{l}{-\frac{m}{2}+mln\sqrt{-m}>0}\\{m<0}\end{array}\right.$⇒-e<m<0.
所以若?x>0,f(x)>0恒成立,则实数m的取值范围是(-e,0).
故?x>0使f(x)≤0成立,实数m的取值范围(-∞,-e]∪(0,+∞).
(3)因为对?x∈[1,m],H′(x)=$\frac{(x-1)(x-m)}{x}$≤0,所以H(x)在[1,m]内单调递减.
于是|H(x1)-H(x2)|≤H(1)-H(m)=$\frac{1}{2}$m2-mlnm-$\frac{1}{2}$,
|H(x1)-H(x2)|<1?$\frac{1}{2}$m2-mlnm-$\frac{1}{2}$<1?$\frac{1}{2}$m-lnm-$\frac{3}{2m}$<0.
记h(m)=$\frac{1}{2}$m-lnm-$\frac{3}{2m}$(1<m≤e),
则h′(m)=$\frac{1}{2}$-$\frac{1}{m}$+$\frac{3}{{2m}^{2}}$=$\frac{3}{2}$($\frac{1}{m}$-$\frac{1}{3}$)2+$\frac{1}{3}$>0,
所以函数h(m)=$\frac{1}{2}$m-lnm-$\frac{3}{2m}$在(1,e]是单调增函数,
所以h(m)≤h(e)=$\frac{e}{2}$-1-$\frac{3}{2e}$=$\frac{(e-3)(e+1)}{2e}$<0,故命题成立.
点评 本题主要考查用待定系数法求函数解析式和根据导数的符号判断函数的增减性的问题.


科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )| A. | 8-2π | B. | 4-$\frac{2π}{3}$ | C. | 8-$\frac{2π}{3}$ | D. | 4-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
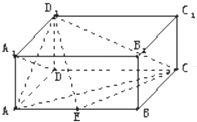 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 7816 | 6572 | 0802 | 6316 | 0702 | 4369 | 9728 | 1198 |
| 3204 | 9234 | 4915 | 8200 | 3623 | 4869 | 6938 | 7481 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com