Question

2．已知函数f（x）=lnx+$\frac{a}{x}$-1，a∈R
（I）若曲线y=f（x）在点（1，f（1））处的切线与直线x-y+1=0垂直，求函数的极值；
（II）当a＞0时，若函数f（x）在区间[1，3]上的最小值为$\frac{1}{3}$，求a的值；
（III）讨论函数g（x）=f′（x）-$\frac{x}{3}$零点的个数．

Answer 1

分析 （I）$f'（x）=\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2}（x＞0）$，利用相互垂直的直线斜率之间的关系、导数的几何意义可得：f'（1）=-1，解得a=2．可得f′（x）=$\frac{x-2}{{x}^{2}}$，再利用导数研究函数的单调性极值即可得出．
（II）对a分类讨论，利用导数研究函数的单调性极值即可得出．
（III）函数$g（x）=f'（x）-\frac{x}{3}=\frac{1}{x}-\frac{a}{x^2}-\frac{x}{3}（x＞0）$．令g（x）=0，得$a=-\frac{1}{3}{x^3}+x（x＞0）$，设$φ（x）=-\frac{1}{3}{x^3}+x（x＞0）$．利用导数研究其单调性极值可得：φ（x）的最大值为$φ（1）=-\frac{1}{3}+1=\frac{2}{3}$．又φ（0）=0，结合y=φ（x）的图象（如图），对a分类讨论即可得出．

解答 解：（I）$f'（x）=\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2}（x＞0）$，
因为曲线y=f（x）在点（1，f（1））处的切线与直线x-y+1=0垂直，所以f'（1）=-1，
即1-a=-1，解得a=2．∴f′（x）=$\frac{x-2}{{x}^{2}}$，
∴当x∈（0，2）时，f'（x）＜0，f（x）在（0，2）上单调递减；
当x∈（2，+∞）时，f'（x）＞0，f（x）在（2，+∞）上单调递增；
∴当x=2时，f（x）取得极小值$f（2）=ln2+\frac{2}{2}-1=ln2$．
∴f（x）极小值为ln2．
（II）当0＜a≤1时，f′（x）＞0在（1，3）上恒成立，这时f（x）在[1，3]上为增函数．
∴f（x）_min=f（1）=a-1，
令 a-1=$\frac{1}{3}$，得a=$\frac{4}{3}$＞1（舍去），
当1＜a＜3时，由f′（x）=0得，x=a∈（1，3），∴φ'（x）=-x²+1=-（x-1）（x+1）
若x∈（1，a），有f′（x）＜0，f（x）在[1，a）上为减函数，
x∈（a，3]，有f′（x）＞0，f（x）在[a，3]上为增函数．
∴f（x）_min=f（a）=lna，令lna=$\frac{1}{3}$，得a=${e}^{\frac{1}{3}}$．
当a≥3时，f′（x）＜0在（1，3）上恒成立，这时f（x）在[1，3]上为减函数，
∴f（x）_min=f（3）=ln3+$\frac{a}{3}$-1．令ln3+$\frac{a}{3}$-1=$\frac{1}{3}$，得a=4-3ln3＜2（舍去）．
综上知，$a={e^{\frac{1}{3}}}$．…（9分）
（III）∵函数$g（x）=f'（x）-\frac{x}{3}=\frac{1}{x}-\frac{a}{x^2}-\frac{x}{3}（x＞0）$
令g（x）=0，得$a=-\frac{1}{3}{x^3}+x（x＞0）$，设$φ（x）=-\frac{1}{3}{x^3}+x（x＞0）$
当x∈（0，1）时，φ'（x）＞0，此时φ（x）在（0，1）上单调递增；
当x∈（1，+∞）时，φ'（x）＜0，此时φ（x）在（1，+∞）上单调递减；
所以x=1是φ（x）的唯一极值点，且是极大值点，因此x=1也是φ（x）的最大值点，∴φ（x）的最大值为$φ（1）=-\frac{1}{3}+1=\frac{2}{3}$．…（11分）
又φ（0）=0，结合y=φ（x）的图象（如图），可知
①当$a＞\frac{2}{3}$时，函数g（x）无零点；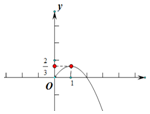
②当a=$\frac{2}{3}$时，函数g（x）有且仅有一个零点；
③当$0＜a＜\frac{2}{3}$时，函数g（x）有两个零点；
④a≤0时，函数g（x）有且只有一个零点； 
综上所述，当a$＞\frac{2}{3}$时，函数g（x）无零点；当a=$\frac{2}{3}$或a≤0时，函数g（x）有且仅有一个零点；当$0＜a＜\frac{2}{3}$时，函数g（x）有两个零点．

点评 本题考查了利用导数研究函数的单调性极值最值及其方程、分类讨论方法、数形结合方法，考查了推理能力与计算能力，属于难题．