
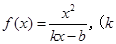 ,
,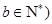 ,满足
,满足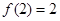 ,
,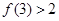 .
.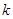 ,
,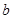 的值;
的值;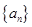 的前
的前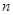 项和为
项和为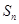 ,且有
,且有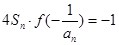 ,设
,设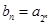 ,求数列
,求数列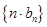 的前
的前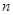 项和
项和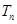 ;
;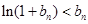 .
.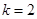 ,
,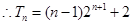
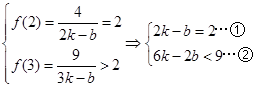 ,
,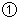 代入
代入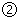 可得
可得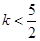 ,且
,且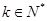 .……………………………………………………2分
.……………………………………………………2分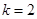 时,
时,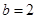 (成立),当
(成立),当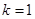 时,
时,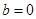 (舍去).
(舍去).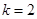 ,
,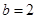 .…………………………………………………………………………4分
.…………………………………………………………………………4分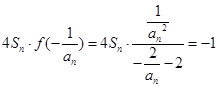 ,即
,即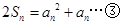 .
.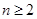 时,
时, 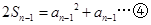 .
.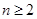 时,由
时,由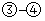 可得
可得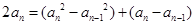 ,
,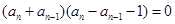 .
.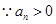 得
得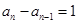 ,且
,且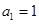 ,
,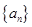 是首项为1,公差为1的等差数列,即
是首项为1,公差为1的等差数列,即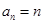 ,
,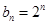 .
.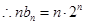 . ………………………………………………………………………………7分
. ………………………………………………………………………………7分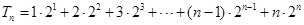 ,
,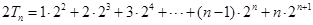 ,
,
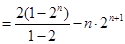 .
.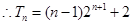 . ……………………………………………………………………10分
. ……………………………………………………………………10分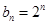 ,只需证
,只需证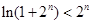 .设
.设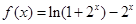 (
(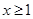 且
且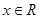 ).
).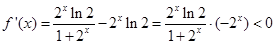 ,
,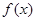 在
在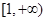 上是递减,
上是递减,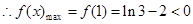 .
.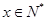 ,则
,则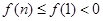 ,
,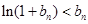 . …………………………………………………………………………14分
. …………………………………………………………………………14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com